Red-Black Tree – 삽입
일명 RB tree라고 부르는 Red Black Tree는 binary search tree의 종류로 모태가 되는 구조는 B tree다. RB tree는 kernel의 메모리를 찾을 때도 사용되고 scheduling 할 때도 많이 사용된다. 큰 장점은 매 새로운 노드를 삽입 / 삭제를 할 때마다 balance 함수를 효과적으로 수행 할 수 있다.
설명
새로운 노드를 삽입 할 때 규칙은 아래와 같은 우선순위로 수행된다.
- root 노드는 언제나 검정이다.
- 새로운 노드는 빨강이다.
- 부모도 빨강, 삼촌도 빨강이면 color flip만 수행
- 부모가 빨강이면 회전한다.
0. 밸런스는 root로부터 모든 leaf로 가는 경로의 검정노드의 수가 같으면 맞는 것으로 간주
1. root 노드는 언제나 검정
반드시 root 노드는 검정색이여야한다. 그래서 처음 노드가 삽입 될 때 해당 노드는 검정색이다.
2. 새로운 노드는 빨강
만약 두 번째로 노드가 삽입 된다고 하면 왼쪽이든 오른쪽이든 빨강색 노드이다.
3. 부모도 빨강, 삼촌도 빨강이면 color flip만 수행
Uncle이 있는 구조일 때는 rotate를 수행하지 않고 color flip만 수행하게 된다.
color flip:
parent, uncle -> BLACK
gparent -> RED
그리고 나서 gparent는 root가 되면서 다시 BLACK으로 바뀐다
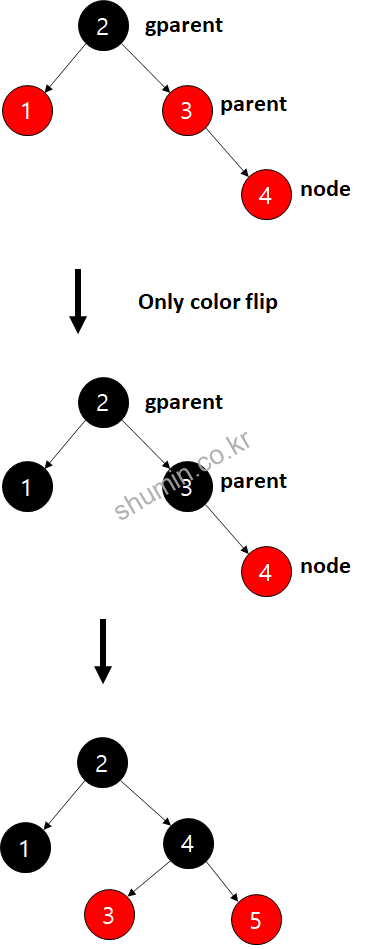
이렇게 계속 5까지 노드가 추가되면 위 그림과 같이 변할텐데, 보면 오른쪽으로 쏠리는 모습으로 되는데 RB tree에선 이 형태도 균형이 맞다고 본다. 왜냐하면 0번 규칙이 있기 때문이다.
4. 부모만 빨강이면 회전
이런 경우는 새로운 노드와 parent 노드가 둘 다 빨강일 경우다. 이 때는 color flip 이 수행된다.
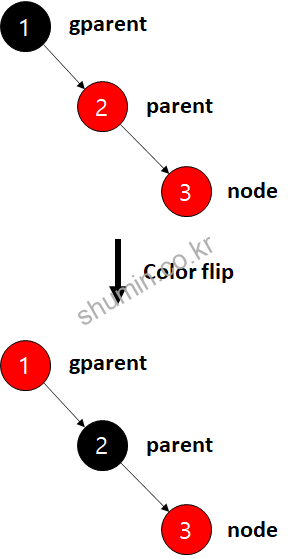
color flip:
parent -> BLACK
gparent -> RED
4.1 R-R 경사
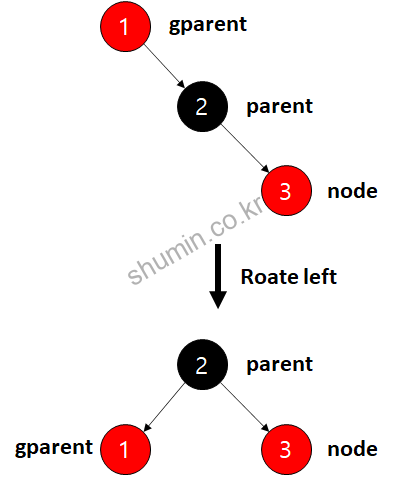
만약 위 그림처럼 노드가 삽입이 되면, parent는 검정, gparent는 빨강이 되는데 오른쪽 – 오른쪽 경사 구조가 되는데, 이럴 때는 오른쪽과 같이 rotate_left가 일어난다.
이 때 gparent를 parent의 왼쪽 자식 노드로 이동시킨다. 만약 아래 그림과 같이 uncle이 있고 새로운 노드가 들어와서 rotate_left가 발생하게 되면 왼쪽으로 경사가 생기는 구조가 된다.
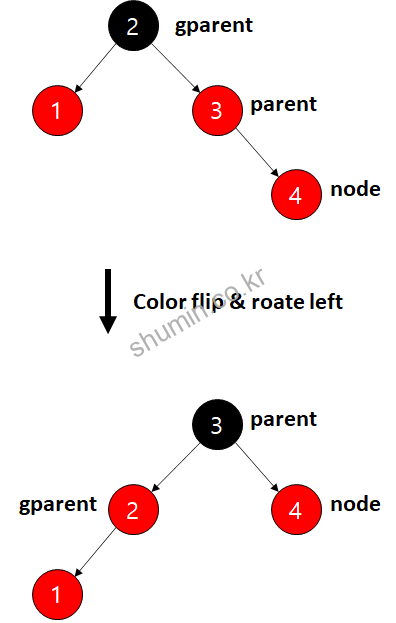
4.2 L-L 경사
만약 왼쪽으로 노드가 자라게 되면 R-R과 반대로 되고, R-R 경사와 같이 roate_right를 수행하게 된다. 그런데 위 그림과 같이 계속 R-R과 L-L 구조의 반복되는 경우가 생겨서 3번 rule이 추가가 필요하다.
0. 밸런스는 root로부터 모든 leaf로 가는 경로의 검정노드의 수가 같으면 맞는 것으로 간주
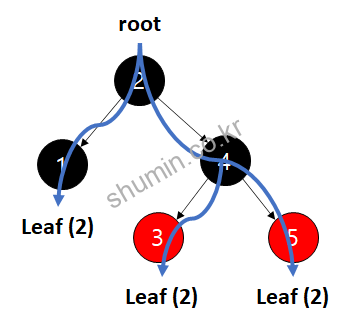
위 그림을 보면 실제 root에서 leaf까지 검정노드의 개수가 모두 동일하다.
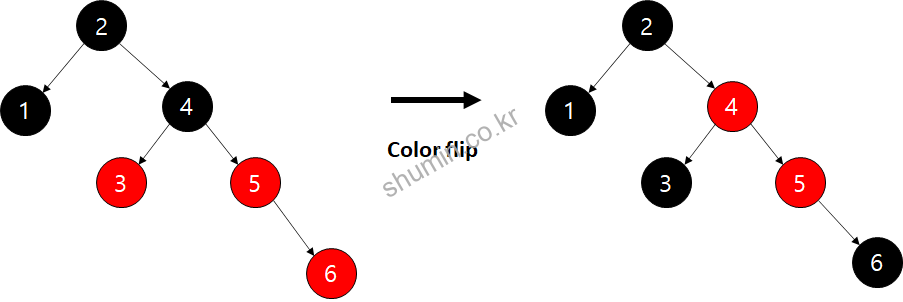
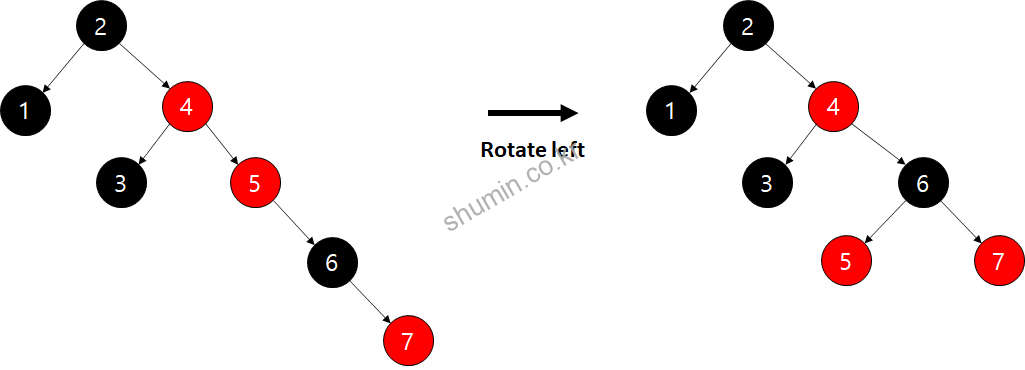
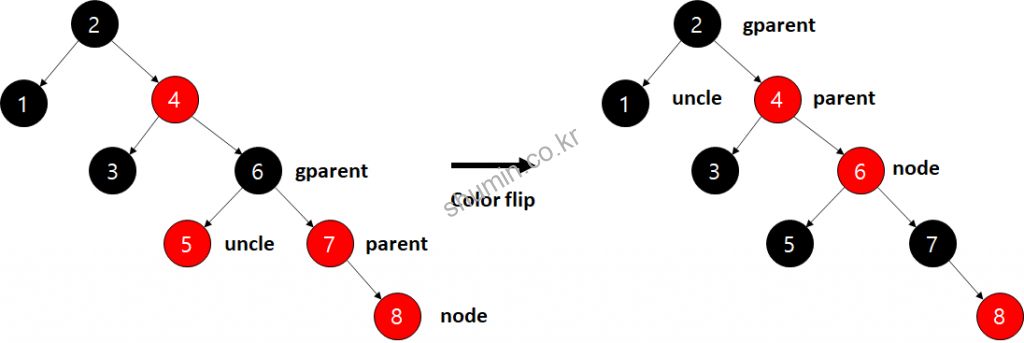
이제 지금까지 나온 규칙을 기반으로 계속 노드가 최가가 되면 7까지 추가가 되면 오른쪽으로 경사가 생긴다. 그러나 8이 들어오는 순간 구조가 달라지게 된다.
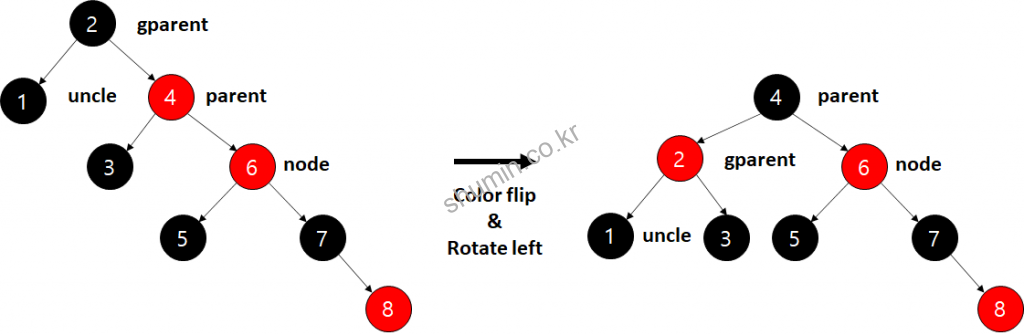
8이 들어오면 3번 규칙에 의해 color flip만 일어나게 되면서, 새로 들어온 노드 기준으로 gparent와 ggparent (할아버지의 아버지)가 모두 빨강 노드가 되면서 4번 규칙에 의해 rorate_left가 일어난다.
구현
기본적으로 generic tree를 기반으로 구현한다.
#include <stdio.h>
#include <stdlib.h>
#include "rbtree.h"
#define INFO_NUM 8
typedef struct {
int data;
struct rb_node node;
} INFO;
typedef struct {
int data;
int color;
} NODE_INFO;
int rb_insert(struct rb_root *root, INFO *info) {
struct rb_node **p = &root->rb_node;
struct rb_node *parent = 0;
INFO *temp;
while(*p) {
// Container_of
parent = *p;
temp = rb_entry( parent, INFO, node);
if(info->data < temp->data)
p = &(*p)->rb_left;
else if(info->data > temp->data)
p = &(*p)->rb_right;
else
return 0;
}
// Insert node
rb_link_node(&info->node, parent, p);
// Balance tree
// rb_insert_color(&info->node, root);
return 1;
}
int __display(struct rb_node *temp, NODE_INFO (*array)[10], int *row, int *col) {
INFO *info;
if(temp == 0)
return 0;
++*row;
__display(temp->rb_left, array, row, col);
info = rb_entry(temp, INFO, node);
array[*row][(*col)].color = temp->rb_color;
array[*row][(*col)++].data = info->data;
__display(temp->rb_right, array, row, col);
--*row;
}
void display(struct rb_root *root) {
int row = -1;
int col = 0;
NODE_INFO a[10][10] = {0,};
__display(root->rb_node, a, &row, &col);
system("clear");
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
if(a[i][j].data) {
if(a[i][j].color == RB_RED)
printf("<%2d>", a[i][j].data);
else
printf("[%2d]", a[i][j].data);
}
else
printf("%4c", ' ');
}
printf("\n");
}
getchar();
}
int main() {
struct rb_root root = {0};
int a[] = {1, 2, 3, 4, 5, 6, 7, 8};
int i;
INFO info[INFO_NUM];
display(&root);
for(i=0; i<INFO_NUM; i++) {
info[i].data = a[i];
rb_insert(&root, info+i);
display(&root);
}
return 0;
}
| < 1> < 2> < 3> < 4> < 5> < 6> < 7> < 8> |
결과는 위 처럼 나오는데, rb_insert 함수 내부에 rb_insert_color를 comment를 지우고 다시 돌리면 아래와 같이 출력하게 된다.
| [ 4] < 2> < 6> [ 1] [ 3] [ 5] [ 7] < 8> |
코드를 설명해보자면, 우선 struct rb_root 타입은 내부에 rb_node의 포인터를 가진다.
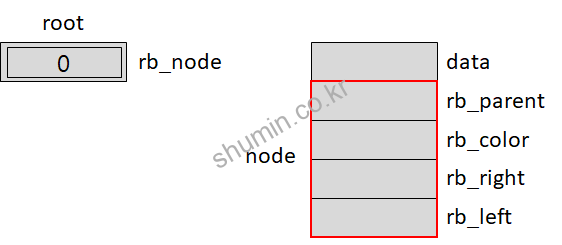
define 구문이 struct 내부에 넣은 것은 가독성을 높이기 위해서다.
기본적으로 INFO 타입은 generic 구조로 노드와 데이터 타입과 무관한 구조로, 내부에 link가 struct rb_node * 타입으로 존재한다.
값을 insert 할 때 struct rb_node ** p가 사용되는데, 이는 p가 가리키는 값인 *p는 처음에 0이 된다. while 문 조건에 2중 포인터를 사용해서 *p를 사용하는 이유는 쓰레기 값을 가지는 pointer로 잘못 접근하는 문제를 방지하기 위해서다.
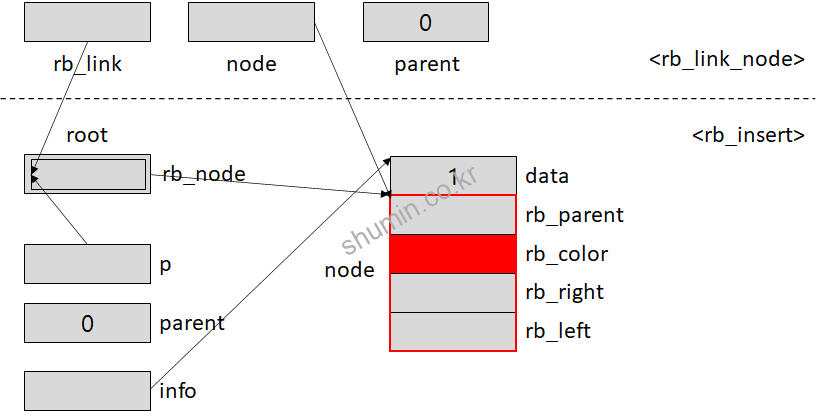
두 번째 노드가 추가될 때부터는 while 내부를 수행하게 되는데, parent는 새롭게 추가되는 node의 부모 node의 generic node쪽의 주소가 저장된다. (parent = *p)
rb_link_node
rb_link_node 함수를 통해 root에 새로운 data의 노드를 연결해준다. 인자로는 총 3개가 들어간다.
1) 새롭게 추가될 구조체 내부 generic node의 주소
2) parent 주소
3) root의 주소 (root가 가리키는 주소가 아닌 root의 주소다.)
color는 기본값으로 RB_RED가 들어간다. 그리고 rb_left와 rb_right는 0으로 초기화해주며, rb_link인 root가 가리키는 값은 새롭게 추가된 node 주소가 된다.
rb_link는 새롭게 추가되기 전 포인터에 주소이기 때문에, *rb_link = node로 새롭게 추가되는 generic node의 주소를 저장시킨다.
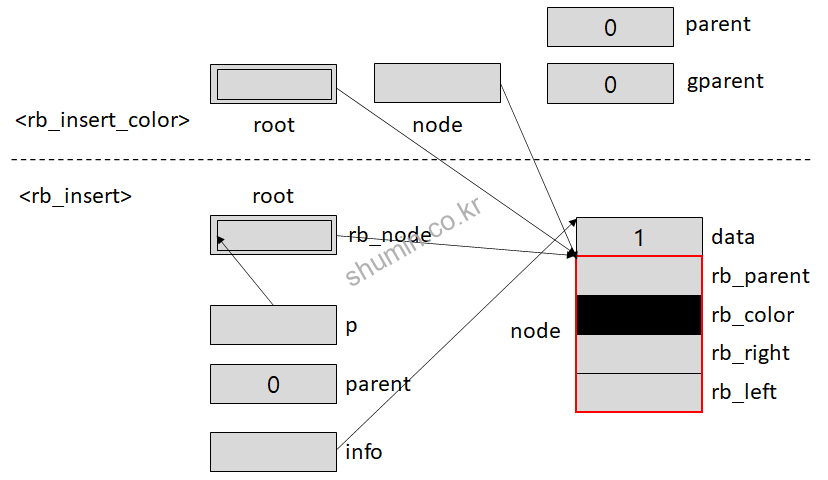
만약 처음 노드의 값이 1이 들어오고, 다음에 2가 들어왔다고 가정하면 두 번째 들어온 2는 1의 값을 가지는 노드의 right에 삽입 될 것이다. 따라서 parent는 이전 노드의 rb_node 주소를, rb_link는 이전 노드의 rb_right를 가리키는 주소이기 때문에, rb_link_node 함수 내부에서 새롭게 추가되는 노드의 주소를 가리키게 된다.
*rb_link = node
rb_insert_color
rb_insert_color 함수는 우리가 위해서 정의해준 RB tree rule에 대해서 동작시키는 balance 함수다. 인자는 총 2개가 들어간다.
1) 새롭게 추가되는 구조체 내부 generic node 주소
2) root node
처음 node가 추가될 때는 첫 while문 조건을 보면 parent를 assign 하게되는데, node->rb_parent는 현재 NULL이기 때문에 while문 진입 없이 바로 끝나고, 가장 아래 코드인 RB tree의 root를 black으로 바꾸는 코드를 수행한다.
while ((parent = node->rb_parent) && parent->rb_color == RB_RED)
root->rb_node->rb_color = RB_BLACK;
두 번째로 2의 값을 가지는 노드가 들어오게 되더라도 while문의 두 번째 조건을 만족시키지 못하기 때문에 또 while문을 수행하지 못하게 된다. 내부 동작이 수행되는 부분은 세 번째 노드로 들어오는 3이 들어올 때다.
3이 들어올 때는 함수 내부에서 사용되는 변수 parent는 2를, gparent는 1의 rb_node를 가리킨다. 그래서 while문 조건인, 1)부모 노드가 존재하고, 2)부모 노드의 색깔이 빨간색인 두 조건이 모두 만족하기 때문에 경사도를 확인하는 조건인 if (parent == gparent->left) 인지를 확인한다.
위에서 계속 설명하는 rb_link_node 함수와 rb_insert_color의 구현은 아래와 같다.
void rb_link_node(struct rb_node * node, struct rb_node * parent, struct rb_node ** rb_link)
{
node->rb_parent = parent;
node->rb_color = RB_RED;
node->rb_left = node->rb_right = 0;
*rb_link = node;
}
void rb_insert_color(struct rb_node * node, struct rb_root * root)
{
struct rb_node * parent, * gparent;
while ((parent = node->rb_parent) && parent->rb_color == RB_RED)
{
gparent = parent->rb_parent;
if (parent == gparent->rb_left)
{
{
register struct rb_node * uncle = gparent->rb_right;
if (uncle && uncle->rb_color == RB_RED)
{
uncle->rb_color = RB_BLACK;
parent->rb_color = RB_BLACK;
gparent->rb_color = RB_RED;
node = gparent;
continue;
}
}
if (parent->rb_right == node)
{
register struct rb_node * tmp;
__rb_rotate_left(parent, root);
tmp = parent;
parent = node;
node = tmp;
}
parent->rb_color = RB_BLACK;
gparent->rb_color = RB_RED;
__rb_rotate_right(gparent, root);
} else {
{
register struct rb_node * uncle = gparent->rb_left;
if (uncle && uncle->rb_color == RB_RED)
{
uncle->rb_color = RB_BLACK;
parent->rb_color = RB_BLACK;
gparent->rb_color = RB_RED;
node = gparent;
continue;
}
}
if (parent->rb_left == node)
{
register struct rb_node * tmp;
__rb_rotate_right(parent, root);
tmp = parent;
parent = node;
node = tmp;
}
parent->rb_color = RB_BLACK;
gparent->rb_color = RB_RED;
__rb_rotate_left(gparent, root);
}
}
root->rb_node->rb_color = RB_BLACK;
}