Red-Black Tree – 삭제

만약 아래 그림과 같은 RB tree 구조가 존재했을 때, node 1을 삭제하면 다음과 같을 것이다.

위 그림과 같이 됐을 때, tree의 균형은 맞는 것 처럼 보일 수 있지만 실제 균형이 맞지 않는 것이다. 왜냐하면 자식 노드가 존재하지 않는 부분은 모두 black으로 취급하기 때문이다.

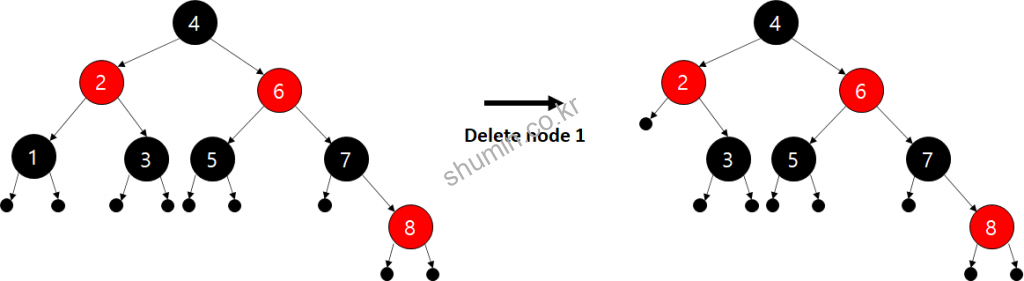
위 그림처럼 다시 본다면 실제 지워진 노드 1 경로에 대해선 검정 노드가 2개밖에 지나지 않는다. 따라서 노드를 삭제 할 때의 룰은 “검정노드를 지울 때 밸런스가 깨진다 “다.

삭제 규칙

1. 형제 노드가 빨강인 경우

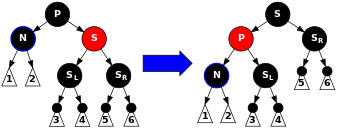
위 그림은 위키피디아에서 가져온 그림인데, 위 그림처럼 지워질 노드인, 나 (N)는 검정이며 형제 노드 (S) 가 빨강일 때 rotate_right (parent)를 수행한다. 이때 당연히 parent와 sibling에 대해서 color flip을 진행을 미리 해줘야한다.

color flip
parent = red
sibling = black
rotate_left (parent)

2. 부모, 형제, 모든 조카가 모두 검정일 경우

위와 같을 때는 형제 노드 (S)만 red로 color flip을 진행한다.

color flip
sibling = red

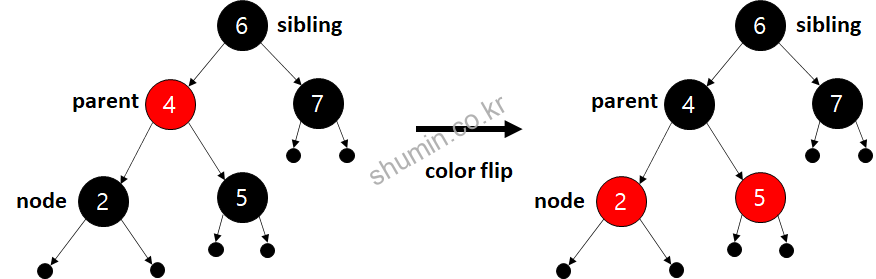
3. 부모가 빨강이고, 형제와 모든 조카가 검정일 경우

부모만 빨강이고 나머지가 검정인 경우다. 이때는 부모와 형제에 대해서 color flip을 진행해준다.

color_flip
parent = black
sibling = red

4. 본인이 왼쪽에 있고, 가까운 위치의 조카가 빨강인 경우

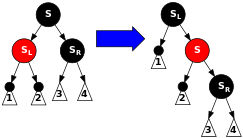
위 그림처럼 조카가 빨강이라는 뜻은 내부적으로 형제는 검정노드라는 의미다. 이 때 수행하는 동작은 가까운 조카는 black으로, 형제는 red로 color flip을 수행하며 rotate_right (sibling) 을 수행해준다.

color_flip
sibling = red
가까운 조카 = black
rotate_right (sibling)

5. 본인 위치 기준으로 먼 조카가 빨강인 경우

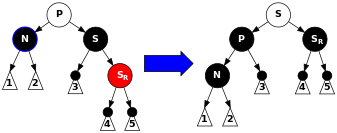
우선 흰색의 의미는 검정 또는 빨강이 모두 될 수 있다. 우선 부모의 색을 black, 형제의 색을 부모의 색으로, 그리고 먼 조카의 색을 black으로 변경하고 난 뒤에 형제 기준으로 부모를 rotate_left 수행해준다.
color flip
parent = black
sibling = parent’s color
먼 조카 = black
rotate_left (parent)

만약 끝 노드가 아니라 중간 노드가 삭제될 경우

삭제하고자 하는 노드를 기준으로 오른쪽에 있는 값 중에 가장 작은 값을 후보로 올린다. 여기서 값만 옮기고, color는 옮기지 않고 그대로 사용한다.

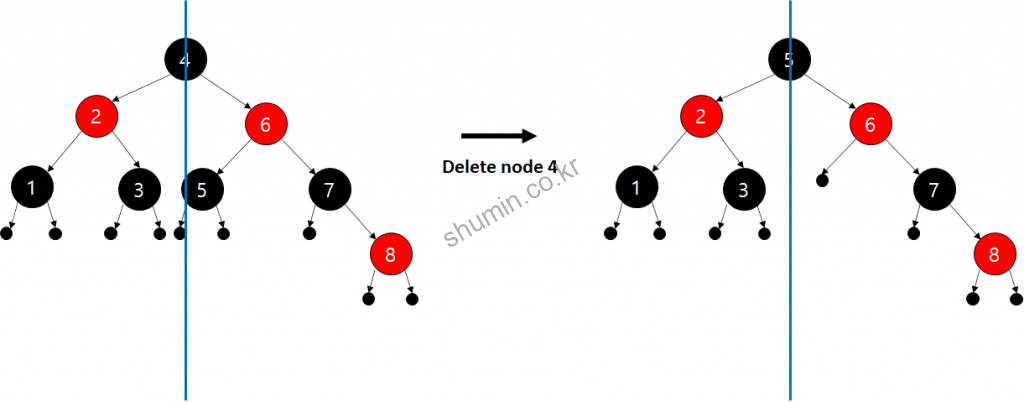
그 후에 규칙 5번에 의해서 parent를 black으로, sibling을 parent’s color로, 먼 조카를 black으로 변경하고 rotate_left를 진행한다.

구현

기존 삽입 코드에 main 구문을 다음과 같이 수정해서 돌려보았다.

int main() {
    struct rb_root root = {0};
    int a[] = {1, 2, 3, 4, 5, 6, 7, 8};
    int i, index;
    INFO info[INFO_NUM];

    for(i=0; i<INFO_NUM; i++) {
        info[i].data = a[i];
        rb_insert(&root, info+i);
    }

    display(&root);
    while(1) {
        printf("Delete node: ");
        scanf("%d", &index);
        rb_erase(&info[index-1].node, &root);
        display(&root);
    }

    return 0;
}

[ 4] < 2> < 6>
[ 1] [ 3] [ 5] [ 7] < 8>

Delete node: 1

위와 같이 나오게 되는데, 만약 node 1을 입력하게 되면 어떻게 변할지 확인해보니 아래와 같이 나왔다.

[ 4] [ 2] < 6>
< 3> [ 5] [ 7] < 8>

Delete node:

위 경우는 3번째 규칙과 같이 부모가 빨강일 때를 의미하기 때문에, 부모를 black으로 형제를 red로 변경하고 본인을 삭제하면 위와 같은 결과를 보여준다.

그 후 3과 8을 삭제하면 아래와 같이 나타난다.

[ 4] [ 2] < 6>
[ 5] [ 7]

Delete node:

여기서 만약 2를 삭제하려고 하면 규칙 1번과 같은데, 이 때 위에서 말한 방식으로 구조가 변경되면 아래 그림과 같이 된다.

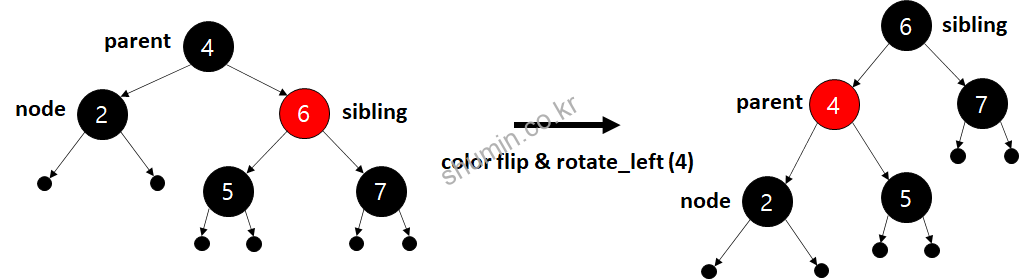
그 후에 다시 부모가 빨강인 규칙 3을 적용하면 아래와 같이 된다.

실제 2를 지운 결과를 보면 아래와 같다.

[ 6] [ 4] [ 7] < 5>

Delete node:

여기서 5는 이미 빨간 노드이기 때문에 바로 지울 수 있다. 여기서 만약 4를 지우고 싶을 때는 규칙 2번과 같이 모든 노드 (나, 부모, 형제)가 검정일 때는 형제 노드를 빨강으로 만들라고 했다. 그럼 노드 4를 지우면 7은 빨강 노드가 될 것이다.

[ 6] < 7>

Delete node:

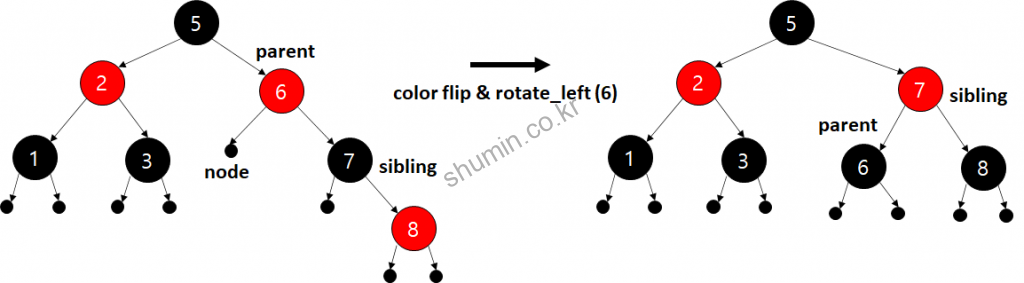
만약 아래 그림과 같이 가까운 조카가 빨강일 경우에 어떻게 지워지는지 보면, 규칙 4처럼 가까운 조카 (5) 기준으로 rorate_right (6)를 수행하게 된다.

그리고 먼 조카가 빨강인 경우 규칙 5처럼 color를 상속받고, rorate_left가 일어나면 아래 그림과 같은 모습이 된다.

Reference

https://ko.wikipedia.org/wiki/%EB%A0%88%EB%93%9C-%EB%B8%94%EB%9E%99_%ED%8A%B8%EB%A6%AC