[Algorithm] Generic Tree
Tree 기본 구조 및 용어
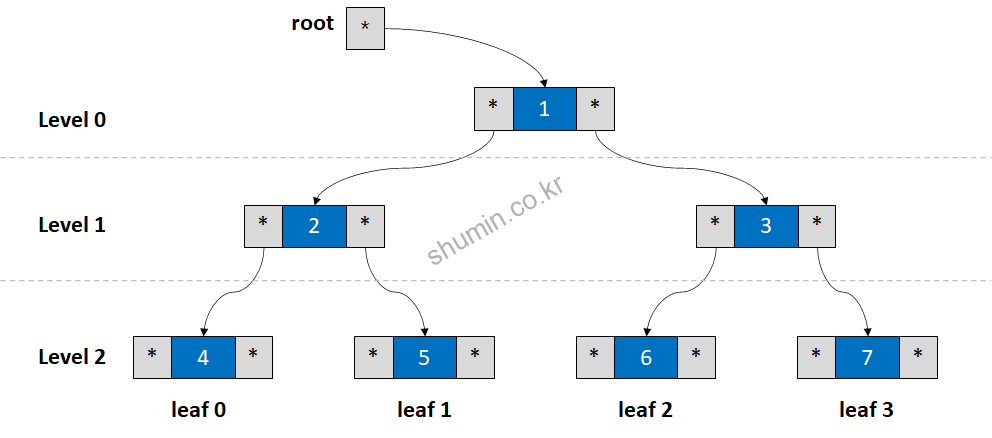
Tree 구조의 특징은 어떤 데이터를 찾고자 할 때 좀 더 빠른 시간 내에 찾을 수 있는 장점을 가진다. 구조는 아래 그림과 같이 root를 기점으로 좌 우 노드와 연결되어 있다.
Tree에서 사용되는 용어 몇 가지가 있는데 다음과 같다.
Root: 최상단 노드
Leaf: 최하단 노드
Level: Root 노드는 0이며, 아래로 갈 수록 level이 높아짐
Depth: 가장 level이 높은 leaf level을 가리키는 말
순회 (Traverse)
Tree를 순회 할 때는 순서가 중요한데, 다음과 같이 root의 순서를 기준으로 3 가지로 나뉜다.
Pre-order Traverse: root -> left -> right
In-order Traverse: left -> root -> right
Post-order Traverse: left -> right -> root
코드
Tree 구조가 위 그림과 같다고 가정한다면 아래처럼 코드를 작성 할 수 있다.
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int data;
struct node *left;
struct node *right;
} NODE;
NODE *root;
typedef enum {LEFT, RIGHT} FLAG;
void insert_data(int data, NODE *s, FLAG flag) {
NODE *temp;
temp = malloc(sizeof(NODE));
temp->data = data;
temp->left = 0;
temp->right = 0;
if(root == 0) {
root = temp;
return;
}
if(flag == LEFT) s->left = temp;
else if(flag == RIGHT) s->right = temp;
}
void pre_order(NODE *temp) {
if(temp == 0)
return;
printf("%d\n", temp->data);
pre_order(temp->left);
pre_order(temp->right);
}
void in_order(NODE *temp) {
if(temp == 0)
return;
in_order(temp->left);
printf("%d\n", temp->data);
in_order(temp->right);
}
void post_order(NODE *temp) {
if(temp == 0)
return;
post_order(temp->left);
post_order(temp->right);
printf("%d\n", temp->data);
}
int main() {
insert_data(1, root, LEFT);
insert_data(2, root, LEFT);
insert_data(3, root, RIGHT);
insert_data(4, root->left, LEFT);
insert_data(5, root->left, RIGHT);
insert_data(6, root->right, LEFT);
insert_data(7, root->right, RIGHT);
in_order(root);
in_order(root);
in_order(root);
return 0;
}
Display 함수
Tree 구조를 display하는 건 쉽지 않다. 따라서 display 함수를 tree 구조에 맞게 구현이 필요하다.
Level 1
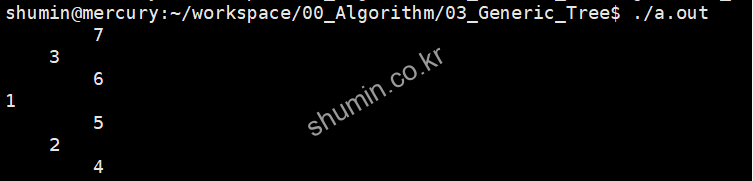
우선 tree를 왼쪽으로 뉘인 것 처럼 display를 하는 방법이 있다. 대신 이 방법으로 하려면 우선 순회 순서를 display 용으로 변경해줘야 한다. 각 하위 노드로 넘어 갈 때마다 indent값을 증가시키면서 출력하는 방법이다.
Display Traverse: right -> root -> left
이렇게 해야 왼쪽으로 눕혔을 때 tree 모습이 나오게 된다.
void display(NODE *temp) {
static int indent = -1;
if(temp == 0)
return;
++indent;
display(temp->right);
for(int i=0; i<indent; i++)
printf("%4c",' ');
printf("%d\n", temp->data);
display(temp->left);
--indent;
}
Level 2
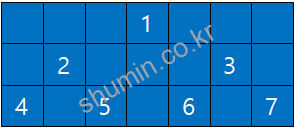
Tree를 눕히지 않고 우리가 보는 모습대로 출력하기 위해선 출력 전에 배열 구조에서 재배치를 한 뒤에 출력하는 방법이다. 이 방식으로 display 하기 위해선 우선 in-order traverse 로 순회하면서 동일하게 하위 노드로 갈 때마다 row를 증가시키고, 값을 쓸 때마다 column을 증가시킨다.
int (*__display(NODE *temp)) [10]{
static int row = -1;
static int col = 0;
static int array[10][10] = {0,};
if(temp == 0)
return array;
++row;
__display(temp->left);
array[row][col++] = temp->data;
__display(temp->right);
--row;
return array;
}
void display(NODE *temp) {
int (*a)[10];
a = __display(temp);
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
if(a[i][j])
printf("%4d", a[i][j]);
else
printf("%4c", ' ');
}
printf("\n");
}
}
shumin@mercury:~/workspace/00_Algorithm/03_Generic_Tree$ ./a.out
1
2 3
4 5 6 7
Level 3
실제 simulator처럼 매 값이 들어 올 때마다 출력이 되도록 하고자 한다. 이를 위해선 row, col, array 변수를 coller로 옮겨주고 내부 display 함수인 __display의 인자로 해당 변수의 주소를 넘겨주면서 해야한다.
int __display(NODE *temp, int (*array)[10], int *row, int *col) {
if(temp == 0)
return 0;
++*row;
__display(temp->left, array, row, col);
array[*row][(*col)++] = temp->data;
__display(temp->right, array, row, col);
--*row;
}
void display(NODE *temp) {
int row = -1;
int col = 0;
int a[10][10] = {0,};
__display(temp, a, &row, &col);
system("clear");
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
if(a[i][j])
printf("%4d", a[i][j]);
else
printf("%4c", ' ');
}
printf("\n");
}
getchar();
}
int main() {
insert_data(1, root, LEFT);
display(root);
insert_data(2, root, LEFT);
display(root);
insert_data(3, root, RIGHT);
display(root);
insert_data(4, root->left, LEFT);
display(root);
insert_data(5, root->left, RIGHT);
display(root);
insert_data(6, root->right, LEFT);
display(root);
insert_data(7, root->right, RIGHT);
display(root);
return 0;
}
1
2 3
4 5 6 7