[Computer Arch.] Floating Point Representation

Computer system에선 대부분 정수가 아닌 수를 표기할 때는 IEEE Standard 754 형식의 floating point 표기 방식으로 표현한다. 이는 1) 기존 binary representation으로 표현할 경우 2의 지수승에 대해서만 정확한 소수가 표현 가능하며, 2) 너무나 작은 수, 또는 너무나 큰 수에 대해서 표현하는데 제약이 되기 때문이다.

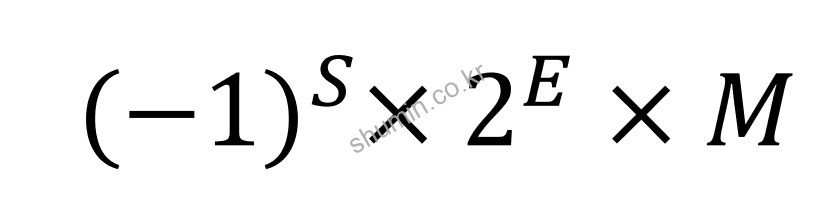
• S: Sign bit
• E: Exponent weight value
• M: [1.0 ~ 2.0) 사이의 값을 나타내는 fraction value

1. Signed Part

S는 보이는 것 처럼 signed bit을 나타낸다. 1이면 negative, 0이면 positive다.

2. Exponent Part

“Exponent”는 크게 세 가지 형태로 분류된다.

1. Normalized values: Exponent != 000…0 and Exponent != 111…1
2. Denormalized values: Exponent == 000…0
3. Special values: Exponent == 111…1

2.1 Normalized values

우선 위쪽 수식에서 E는 E = Exponent - Bias로 표현되는데, Exponent는 8-bit으로 나타낼 수 있는 숫자이며, Bias는 2^(k-1)-1인 값이다. Single precision의 경우 127이 Bias가 된다. 즉, 32-bit single precision의 경우 E = Exponent - 127가 된다.

2.2 Denormalized values

Exponent가 0인 경우에 denormalized value로 표현되는데, 더 세밀한 소수점 값을 표현할 때 사용된다. 즉, 0에 더 가까운 값이다.

E = 1 - Bias로, single precision의 경우 Bias는 127이기 때문에 2^(-126)이 된다.

2.3 Special values

Exponent = 111...1로 설정된 경우에 나타나며, infinity, Not-A-Number (NaN)를 표현할 때 사용된다.

따라서 위 경우들을 조합해서 그려보면 위와 같다.

3. Fraction Part

최소 1.0, 최대 2.0 – delta 로 표현되는 이 값은 항상 1.xxx…x로 표현된다.

4. Example

• S = 0
• Exponent = 140
• Fraction = 0b1101…0

만약 위 처럼 각 field의 값이 저렇게 정해진다면, 아래 표현식처럼 계산이 될 것이다.