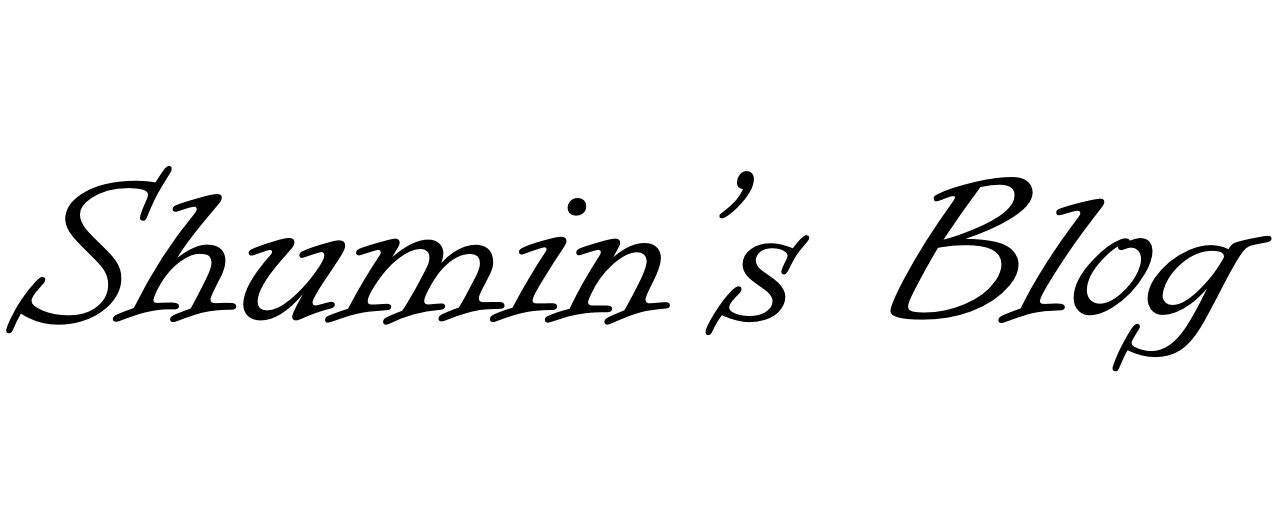Binary Search Tree
일반적인 Tree는 검색용으로 적합하지 않다. 왜냐하면 어떤 값을 tree 구조에 저장 할 때 항상 tree에 노드가 균일하게 배치가 된다는 보장이 없기 때문이다.
이를 위해서 Binary Search Tree 구조는 balance 함수를 통해서 항상 log(2)N의 성능을 보장하도록 한다. 이 balance 함수가 key point다.
Binary Search Tree의 주의사항은 중복된 data 값은 절대 허용이 안된다.
새로운 데이터를 가지는 노드를 넣을 때는 root부터 값을 비교해서, 새로운 값이 현재 가리키고 있는 tree node의 값보다 작을 경우 왼쪽에, 클 경우에 오른쪽 노드로 이동시킨다. 최종적으로 tree node를 가리키는 포인터가 null인 경우 traverse를 멈추고 노드 아래에 연결시켜준다.
작성된 코드는 아래와 같이 될 수 있다.
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int data;
struct node *left;
struct node *right;
} NODE;
NODE *root;
typedef enum {LEFT, RIGHT} FLAG;
void insert_data(int data) {
NODE *temp;
NODE *p = root;
NODE *prev;
temp = malloc(sizeof(NODE));
temp->data = data;
temp->left = 0;
temp->right = 0;
if(root == 0) {
root = temp;
return;
}
while(p) {
prev = p;
if(p->data > data)
p = p->left;
else if(p->data < data)
p = p->right;
else
return;
}
if(prev->data > data)
prev->left = temp;
else
prev->right = temp;
}
int __display(NODE *temp, int (*array)[10], int *row, int *col) {
if(temp == 0)
return 0;
++*row;
__display(temp->left, array, row, col);
array[*row][(*col)++] = temp->data;
__display(temp->right, array, row, col);
--*row;
}
void display(NODE *temp) {
int row = -1;
int col = 0;
int a[10][10] = {0,};
__display(temp, a, &row, &col);
system("clear");
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
if(a[i][j])
printf("%4d", a[i][j]);
else
printf("%4c", ' ');
}
printf("\n");
}
getchar();
}
int main() {
int a[] = {4, 2, 1, 3, 6, 5, 7};
int i;
display(root);
for(i=0; i<7; i++) {
insert_data(a[i]);
display(root);
}
return 0;
}
개선된 insert_data 함수
위 코드에서 insert_data함수는 비효율적인 부분이 있는데, 1) root가 null인 경우는 많지 않은데 계속 반복해줘야한다.
추가로 2) prev에 매번 p 값을 저장해줘야하는 불필요한 연산이 들어간다. 이 두 가지를 제거할 수 있다.
p를 root의 값을 저장하는게 아니라 root의 포인터를 가리키도록 하면 된다. 아래처럼 p의 값을 변경함으로 if (root == 0) 부분을 날릴 수 있다.NODE **p = &root;
기존에 p = prev; 부분을 매번 수행하는것과 달리, 이렇게 p에 포인터를 가리키는 부분의 주소를 담게 되면 traverse를 탈출하더라도 주소를 알 수 있다. 따라서 최종적으로 노드의 left, right를 결정하는 코드를 제거 할 수 있다.
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int data;
struct node *left;
struct node *right;
} NODE;
NODE *root;
typedef enum {LEFT, RIGHT} FLAG;
void insert_data(int data) {
NODE *temp;
NODE **p = &root;
temp = malloc(sizeof(NODE));
temp->data = data;
temp->left = 0;
temp->right = 0;
while(*p) {
if((*p)->data > data)
p = &(*p)->left;
else if((*p)->data < data)
p = &(*p)->right;
else
return;
}
*p = temp;
}
int __display(NODE *temp, int (*array)[10], int *row, int *col) {
if(temp == 0)
return 0;
++*row;
__display(temp->left, array, row, col);
array[*row][(*col)++] = temp->data;
__display(temp->right, array, row, col);
--*row;
}
void display(NODE *temp) {
int row = -1;
int col = 0;
int a[10][10] = {0,};
__display(temp, a, &row, &col);
system("clear");
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
if(a[i][j])
printf("%4d", a[i][j]);
else
printf("%4c", ' ');
}
printf("\n");
}
getchar();
}
int main() {
int a[] = {4, 2, 1, 3, 6, 5, 7};
int i;
display(root);
for(i=0; i<7; i++) {
insert_data(a[i]);
display(root);
}
return 0;
}
Balance 기능
BST는 각 leaf node가 모두 같은 level을 가져야 성능이 좋다. 만약 1 – 2 – 3 – 4 – 5 – 6 – 7 이런식으로 insert가 되면 한쪽으로 기울어진 tree가 되면서, 결국 linked list 구조와 똑같이 되면서 시간복잡도가 log2N이 아니라 N만큼 되기 때문에 tree로서 가치가 떨어진다
따라서 모든 노드가 level이 최대한 같도록 balance를 맞추도록 해야한다.
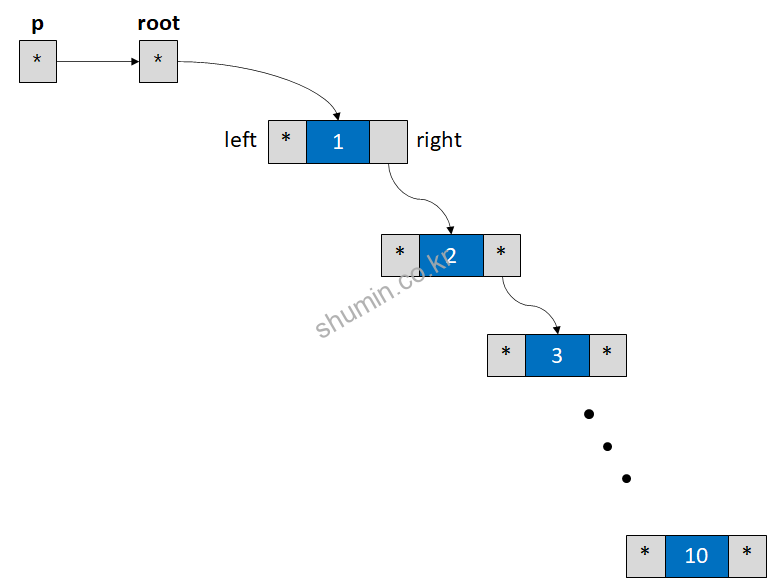
우선 쉽게 각 노드의 순서를 관리하기 위해 배열을 통해 관리하는 방식을 사용한다.
우선 중간값을 가지고 기준 노드를 찾아야한다.
이 때 내부 함수 __bal(a, n)을 통해 배열에 저장한 값을 통해 노드 balance를 맞춘다.
a는 array 주소가, n은 노드의 최대 개수를 전달한다.
void __bal(int *a, int n) {
int mid;
NODE *temp;
mid = n/2;
temp = malloc(sizeof(NODE));
temp->data = a[mid];
temp->left = __bal(a, mid);
temp->right = __bal(a+mid+1, n-mid-1);
}
Balance 함수의 핵심 코드는 위와 같이, mid 값은 전체 노드 개수의 절반을 나눈 값으로 정하고, 해당 index값을 기준으로 왼쪽과 오른쪽 array들에 대해서 재귀적으로 호출시킨다.temp->left에 __bal(a, mid)를 통해 왼쪽 부분을, temp->right에 __bal(a+mid+1, n-mid-1)를 통해 가운데 노드의 오른쪽 부분을 연결시킬 수 있도록 호출한다.
해당 함수의 종료 조건은 n의 값은 반드시 0보 커져야한다.
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
int data;
struct node *left;
struct node *right;
} NODE;
NODE *root;
typedef enum {LEFT, RIGHT} FLAG;
void insert_data(int data) {
NODE *temp;
NODE **p = &root;
temp = malloc(sizeof(NODE));
temp->data = data;
temp->left = 0;
temp->right = 0;
while(*p) {
if((*p)->data > data)
p = &(*p)->left;
else if((*p)->data < data)
p = &(*p)->right;
else
return;
}
*p = temp;
}
int __display(NODE *temp, int (*array)[10], int *row, int *col) {
if(temp == 0)
return 0;
++*row;
__display(temp->left, array, row, col);
array[*row][(*col)++] = temp->data;
__display(temp->right, array, row, col);
--*row;
}
void display(NODE *temp) {
int row = -1;
int col = 0;
int a[10][10] = {0,};
__display(temp, a, &row, &col);
system("clear");
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
if(a[i][j])
printf("%4d", a[i][j]);
else
printf("%4c", ' ');
}
printf("\n");
}
getchar();
}
void __fill(NODE *temp, int *a, int *n) {
if(temp == 0)
return;
__fill(temp->left, a, n);
a[(*n)++] = temp->data;
__fill(temp->right, a, n);
}
NODE* __bal(int *a, int n) {
int mid;
NODE *temp;
if(n<=0)
return 0;
mid = n/2;
temp = malloc(sizeof(NODE));
temp->data = a[mid];
temp->left = __bal(a, mid);
temp->right = __bal(a+mid+1, n-mid-1);
return temp;
}
void bal(NODE *temp) {
int a[100];
int n=0;
__fill(temp, a, &n);
root = __bal(a, n);
}
int main() {
int a[] = {7, 6, 5, 4, 3, 2, 1};
int i;
for(i=0; i<7; i++) {
insert_data(a[i]);
}
display(root);
bal(root);
display(root);
return 0;
}
이 코드의 가장 큰 단점은 실시간 balance가 되지 않는점이다. 해당 코드는 주기적으로 호출이 되어야하는 단점이 있다.