[Algorithm] Knuth-Morris-Pratt (KMP) 알고리즘
효과적인 설명을 위해 notation은 다음과 같다.x: 찾고자 하는 문자열m: x의 길이y: 본문의 문자열n: y의 길이
Morris-Pratt 알고리즘은 패턴 매칭을 하는데 유용한 알고리즘 중 하나다. Shift OR 함수처럼 매칭 시작전에 lookup table을 만드는 작업이 필요하다.
Lookup Table 만들기
void preKmp(char *x, int m, int kmpNext[]) {
int i, j;
i = 0;
j = kmpNext[0] = -1;
while (i < m) {
while (j > -1 && x[i] != x[j])
j = kmpNext[j];
i++; j++;
kmpNext[i] = j;
}
}
preKmp() 함수는 lookup table을 사전에 만드는 함수다. 내부엔 2중 while loop이 존재하는데, i는 찾는 단어의 문자열 index, j는 kmpNext array의 index를 가리킨다. kmpNext가 우리가 만들어야 하는 array인데, 이 값의 의미는 우리가 찾는 단어의 첫 단어부터 i번째 단어까지 일치하는 접두사 – 접미사의 최대 길이를 말한다. 따라서 위 코드는 그 값을 나타낼 수 있도록 하는 알고리즘이다.
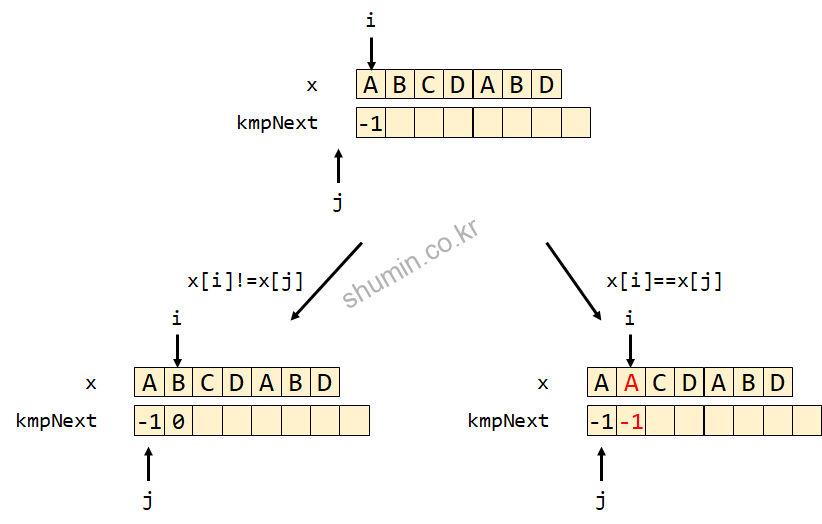
먼저 찾고자 하는 단어가 ABCDABD라고 가정하고 설명한다.j는 처음 -1로 시작하며 kmpNext[0] 값 또한 -1이다. 내부 while (j > -1 && x[i] != x[j])를 만족시키지 못하기 때문에 i, j를 증가시키면서 현재 문자와 다음 문자가 다르기 때문에 kmpNext[1]에 0을 저장한다. 만약 같다면 0이, 다르면 -1이 저장될 것이다.
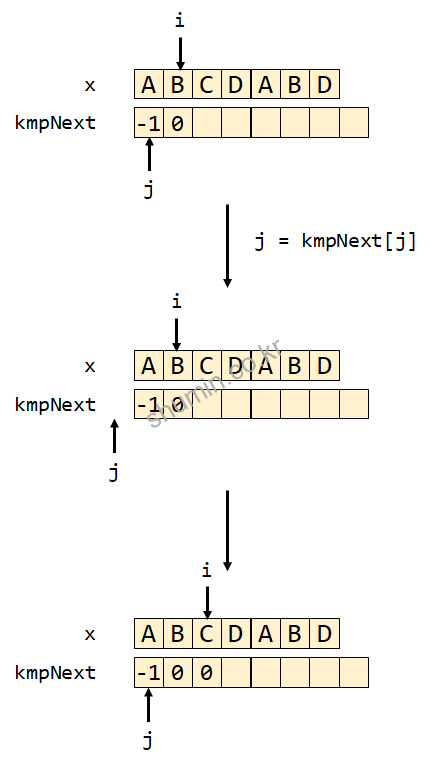
j는 0이 되면서 while (j > -1 && x[i] != x[j]) 조건을 만족시면서 (x[0]과 x[1]이 다른 글자인지 확인), j에 kmpNext[0]인 -1을 다시 넣어서 초기값으로 돌아간다. 그리고 다시 i와 j의 index를 다시 증가시키면서 mpNext[2] = 0을 수행한다.
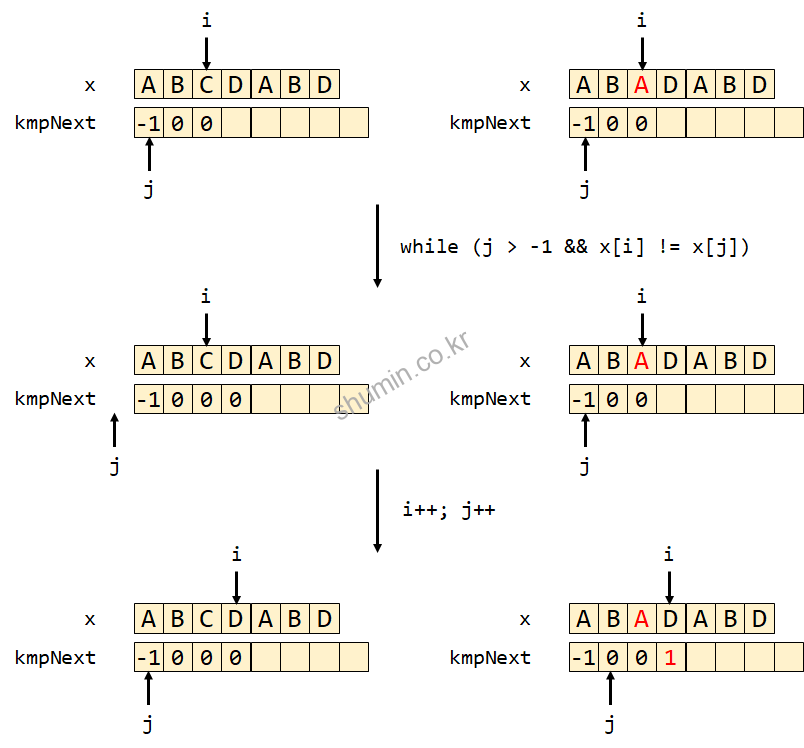
만약 3번째 단어가 1번째 단어와 같을 경우 어떻게 kmpNext가 변하는지 보면, while문을 타지 않으면 j가 -1로 업데이트되지 않으면서 kmpNext[3]에 1이 저장된다. 이 뜻은 첫 번째 단어와 index에 해당하는 마지막 단어가 1개가 일치한다는 뜻이다.
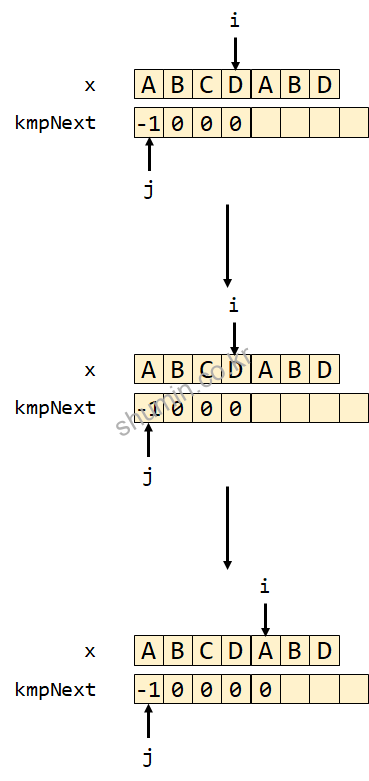
다음과 다음다음 iteration도 동일하게 i가 1씩 증가하고 kmpNext[3], kmpNext[4]의 값도 0이 저장된다. 그리고 다른 동작은 다음에 나타난다.
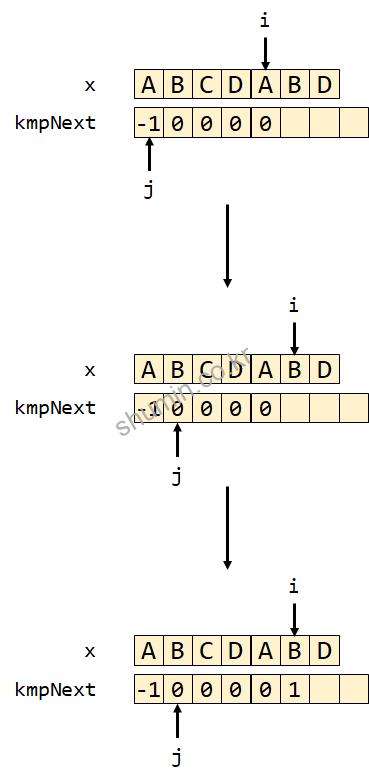
while (j > -1 && x[i] != x[j])를 만족하지 않기 때문에 j를 업데이트하지 않고 넘어가면서 kmpNext[5]=1이 수행된다.
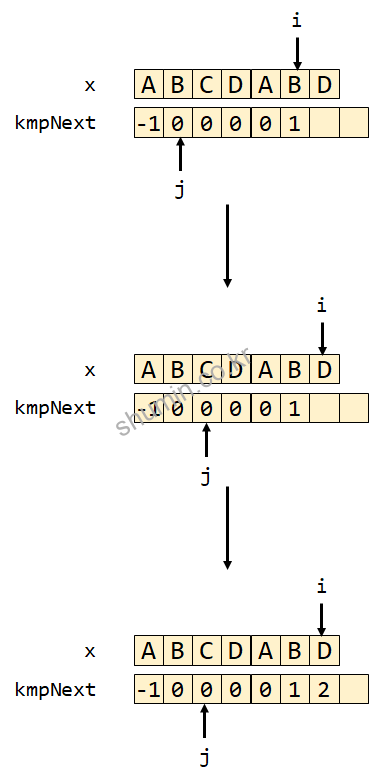
그리고 다음 index인 i가 D를 가리키게 될 때도 동일하게 수행되면서 kmpNext[6]의 값은 2가 된다. 즉 D 이전까지 문자열에 접두사와 접미사가 동일한 문자의 길이는 2라는 의미다.
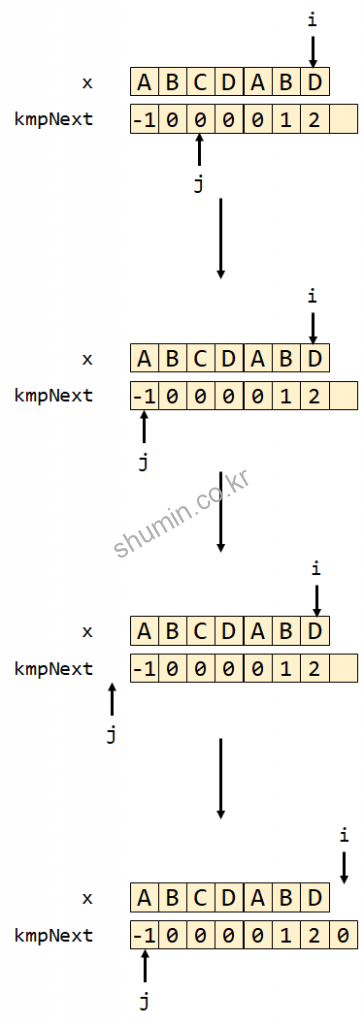
마지막 iteration을 보면 x[i]와 x[j]가 다르기 때문에 while문을 통해서 j는 -1로 돌아가고 kmpNext[7]엔 0이 쓰이면서 함수가 종료된다.
Matching
이렇게 접두사, 접미사의 수를 기록해놓은 lookup table을 만든 이유는 우리가 불필요한 matching 동작을 줄이려고 하는 것이다.
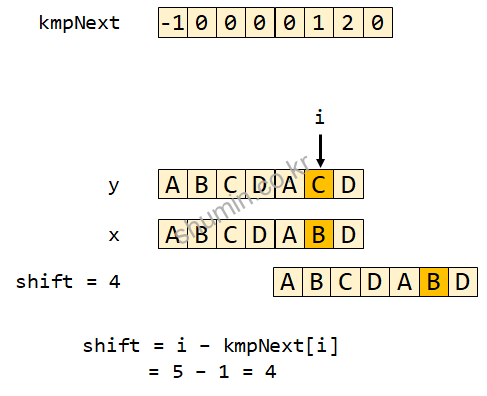
위 그림에서 y가 본문 문자열이라고 하면 6번째 글자가 일치하지 않는다고 했을 때, kmpNext의 값을 index 값에서 뺀 결과를 shift 수로 이용할 수 있다.
void KMP(char *x, int m, char *y, int n) {
int i, j, mpNext[XSIZE];
/* Preprocessing */
preKmp(x, m, mpNext);
/* Searching */
i = j = 0;
while (j < n) {
while (i > -1 && x[i] != y[j])
i = mpNext[i];
i++;
j++;
if (i >= m) {
OUTPUT(j - i);
i = mpNext[i];
}
}
}
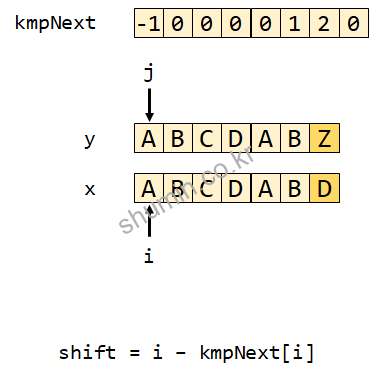
만약 위와 같은 문자와 본문을 KMP 함수를 통해 비교한다고 했을 때, while (i > -1 && x[i] != y[j])는 계속 만족시키지 못했다가 틀린 문자가 찾아졌을 때 while구문을 수행한다.
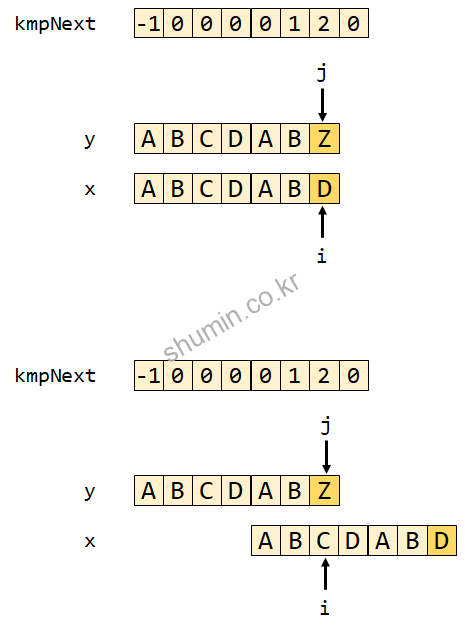
i를 변경하면 위 그림처럼 x 전체가 shift 된 것 같이 된다. 즉 우리가 구한 shift 값인 6 – 2 = 4인 4칸을 뒤로 shift 한 것과 같은 동작을 수행한다. 즉 우리는 lookup table에 접두사와 동일한 접미사의 길이를 알기 때문에 해당하는 접미사부터 다시 비교를 시작하는 것이다.
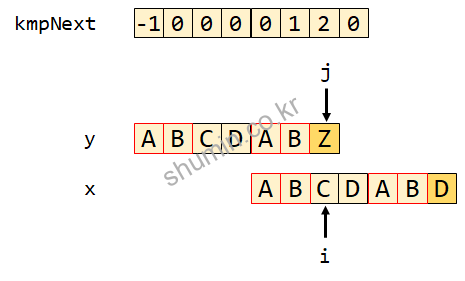
그리고 while문을 통해서 x의 index인 i를 계속 옮겨주면서 x를 밀어주면서 비교를 진행한다.
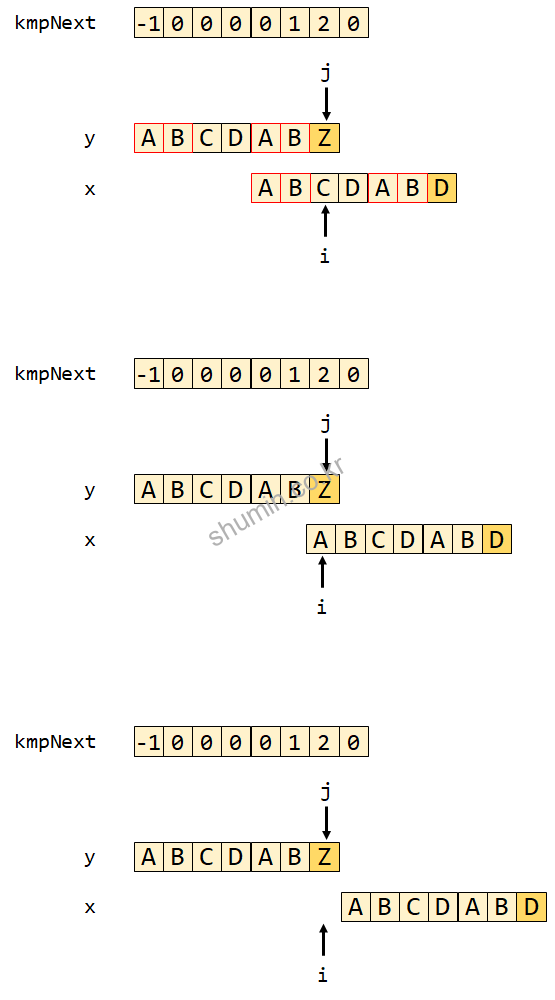
MP to KMP
우리가 사실 지금 설명한 알고리즘은 정확히는 KMP의 이전 알고리즘인 MP (Morris-Pratt)에서 향상시킨 것이다.
void preKmp(char *x, int m, int kmpNext[]) {
int i, j;
i = 0;
j = kmpNext[0] = -1;
while (i < m) {
while (j > -1 && x[i] != x[j])
j = kmpNext[j];
i++; j++;
// kmpNext[i] = j;
if (x[i] == x[j])
kmpNext[i] = kmpNext[j];
else
kmpNext[i] = j;
if(i > 6) {
printf("i=%d, j=%d\n", i, j);
display(kmpNext, m);
}
}
}
위 코드에서 보면 kmpNext[i] = kmpNext[j]; 부분이 추가된 것을 볼 수 있다. 이 차이는 lookup table을 만드는데 미리 비교를 하는 의미를 가진다. 즉 어차피 index를 비교해도 처음 match가 되지 않을 시에는 아예 첫 문자부터 비교를 진행해야한다는 기술이 담겨있다.
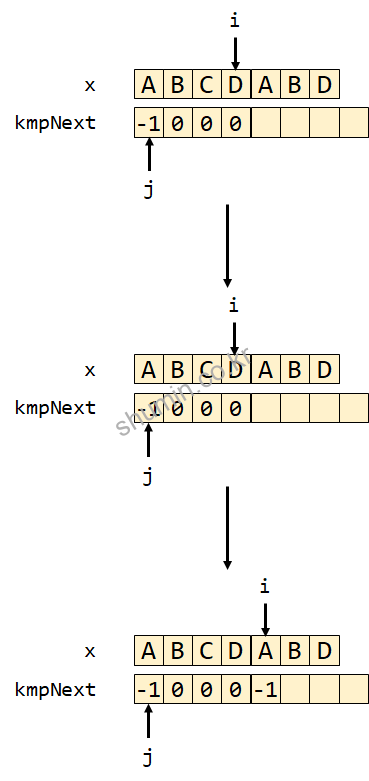
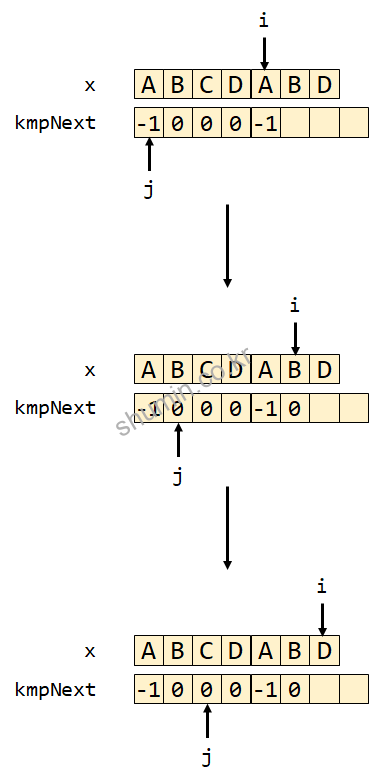
preKmp 함수에서 5번째 단어 A에 해당하는 kmpNext[4]에 -1이 들어가고, kmpNex[5]는 0이 들어간다.
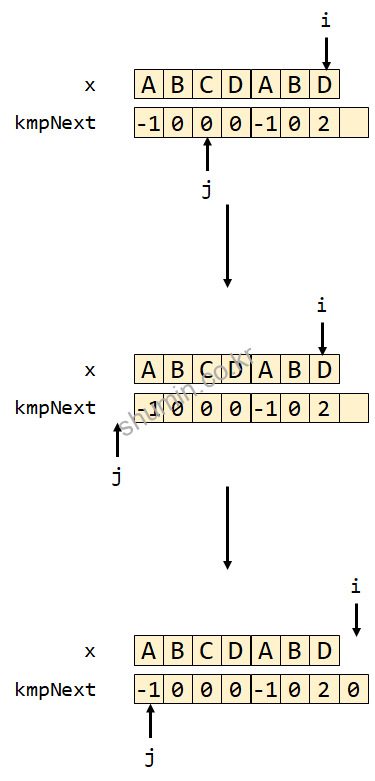
나중에 matching을 할 때는 kmpNext의 값을 활용해서 iteration 수가 결정되는데, 수가 작으면 작을 수록 x의 index 위치를 앞으로 당겨서 비교 수를 줄일 수 있다. 결과는 KMP 알고리즘이 더 시간을 줄이는데 이점을 가진다.
Reference
- https://m.blog.naver.com/kks227/220917078260
- http://www-igm.univ-mlv.fr/~lecroq/string