Introduction (including Spanning Tree)

Kruskal 알고리즘이란 최소한의 비용으로 다수의 노드를 연결을 greedy하게 할 때 사용하는 알고리즘이다. 이 알고리즘은 보통 Spanning Tree를 만들 때 사용되는데, Spanning Tree란 graph 구조에서 모든 vertex가 서로 연결이 되는데 최소한의 edge로 연결을 시킨 graph를 말한다. 따라서 Spanning Tree가 되기 위한 조건은 다음과 같다.

총 Vertex의 수 = 총 Edge의 수 + 1

그렇다면 최소한의 비용으로 구성되는 Spanning Tree를 Minimum Spanning Tree (MST)라 부르는데, MST를 만드는 방법을 알아보면 간략하게 다음 과정을 거친다.

Algorithm

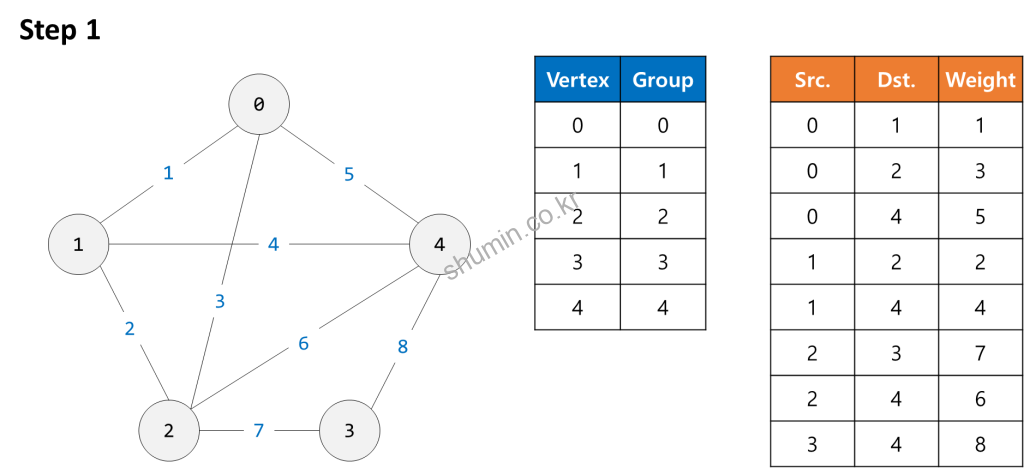
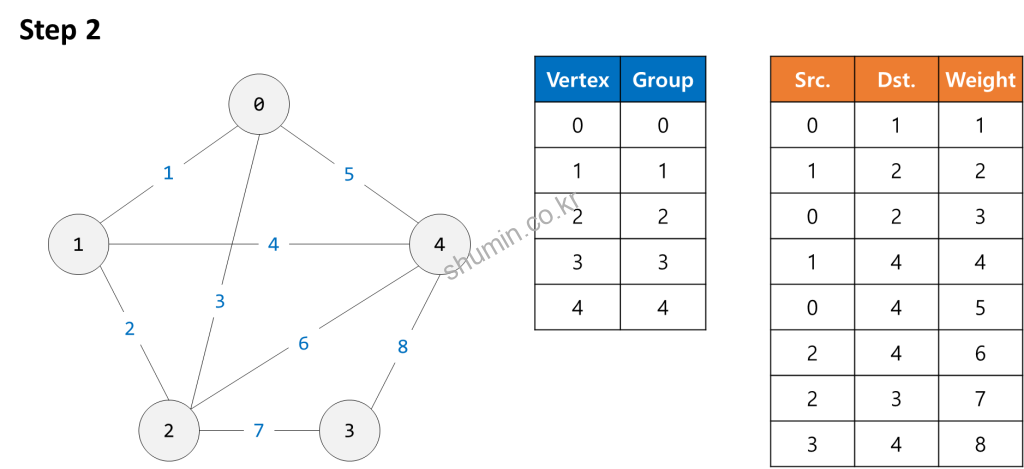
1. Graph의 edge들을 가중치를 작은 것부터 큰 순서대로 오름차순으로 정렬한다.
2. 가장 가중치가 낮은 edge부터 추가하면서 graph를 만든다.
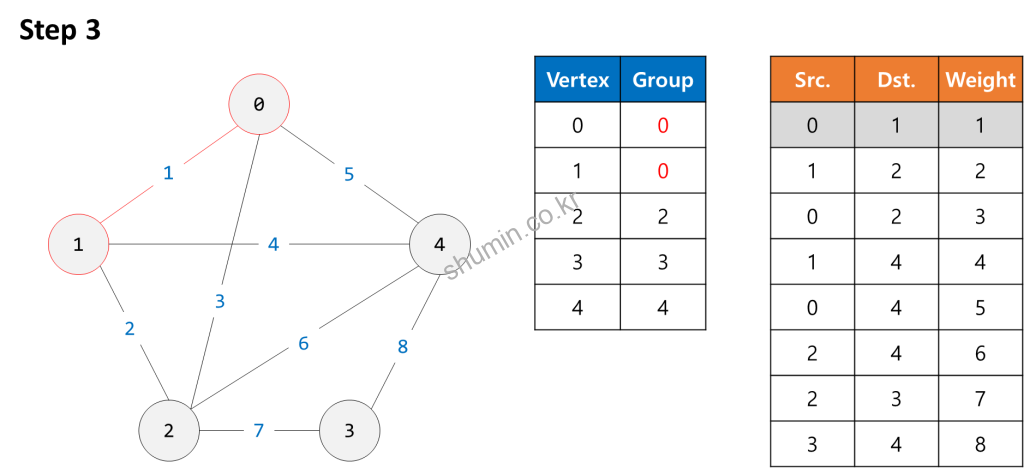
3. 만약 edge를 추가하다가 cycle이 발생되면 해당 edge는 제외한다.
4. Cycle이 발생되는지 확인 방법은 edge의 source vertex의 그룹과 종료 destination vertex의 그룹이 같으면 cycle이 발생되는 것이라 판단 가능하다.
5. Edge의 수가 vertex의 수보다 1개 적으면 종료한다.

Example

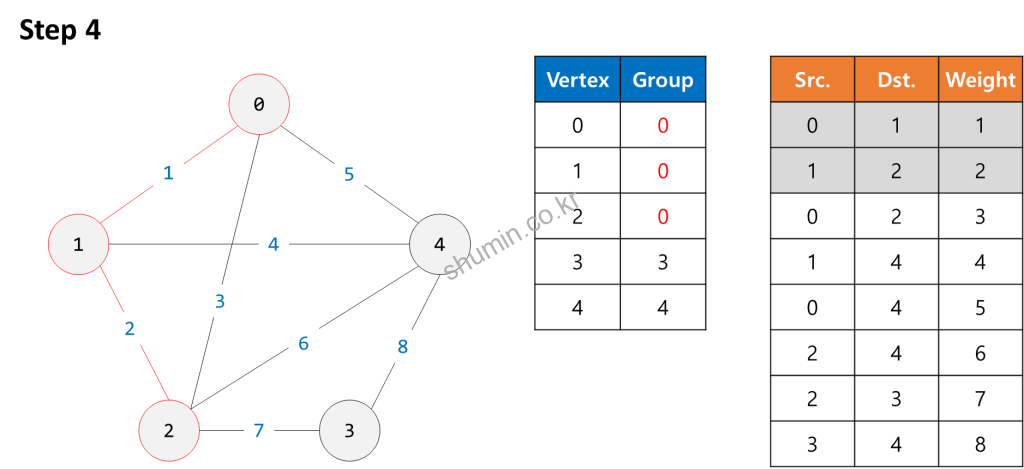
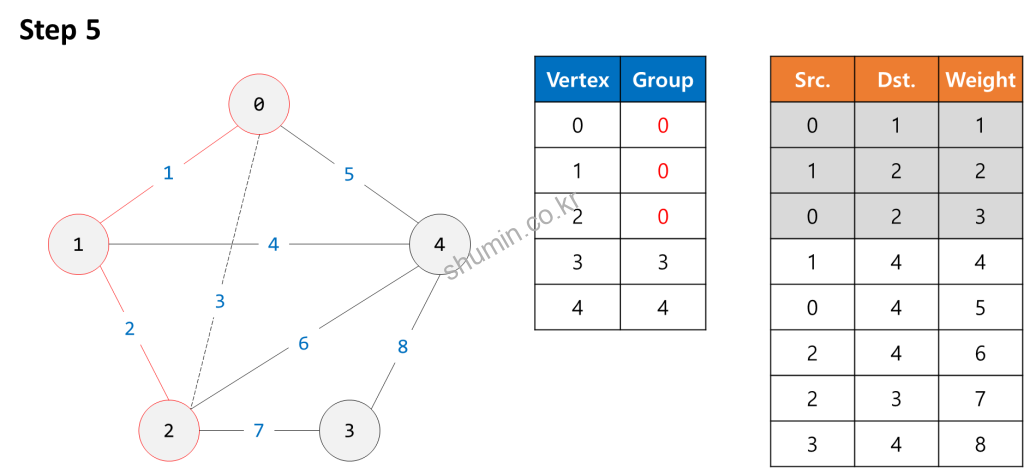
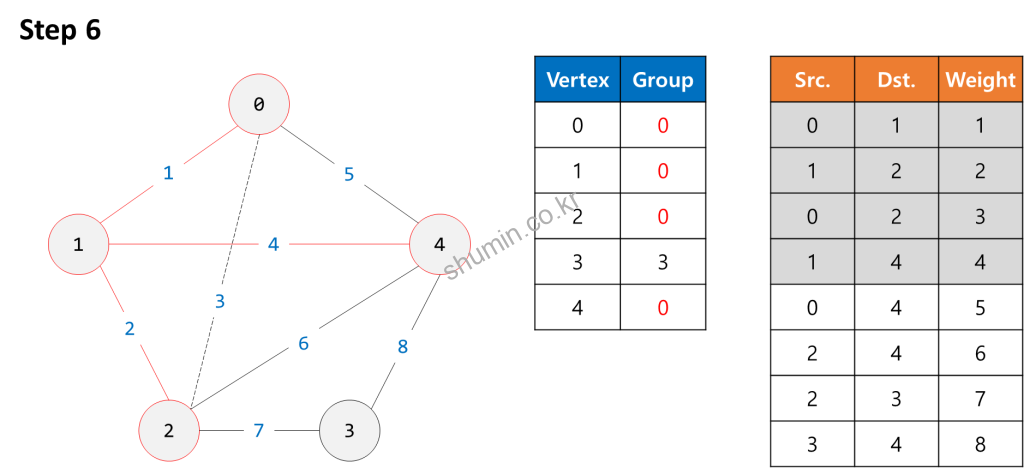
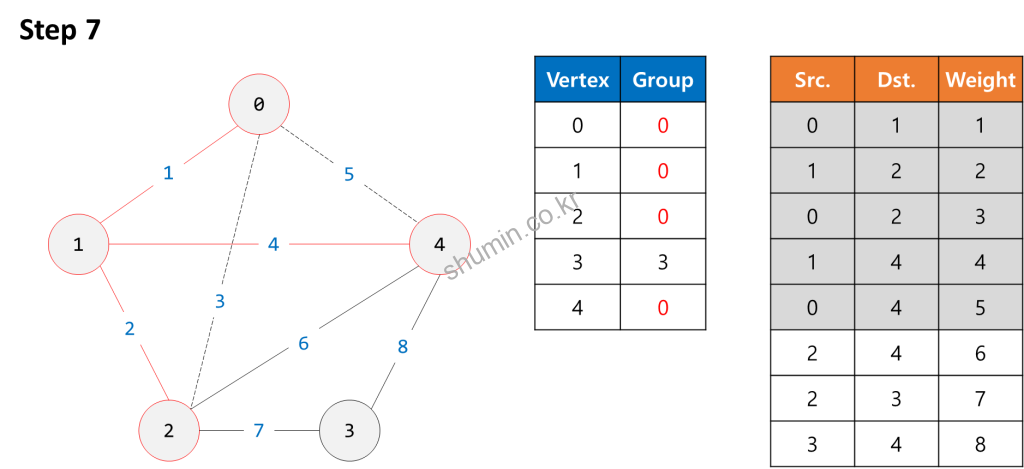
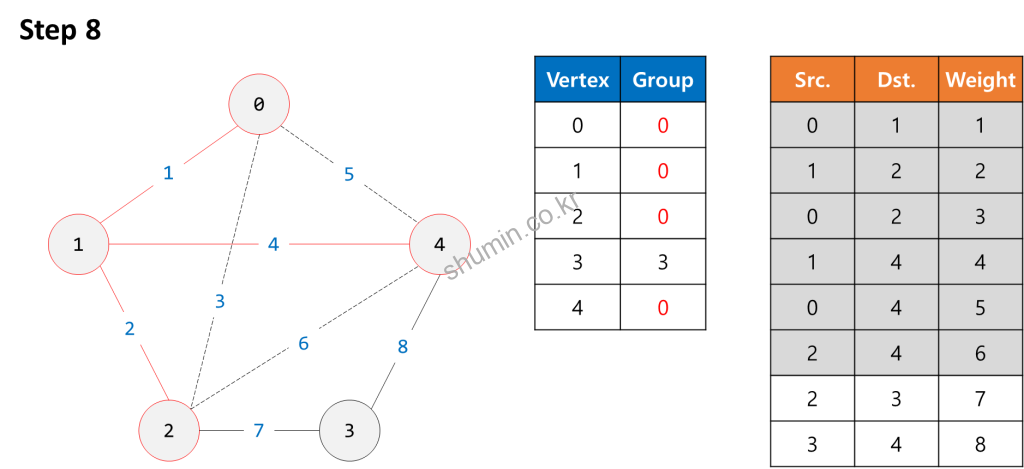
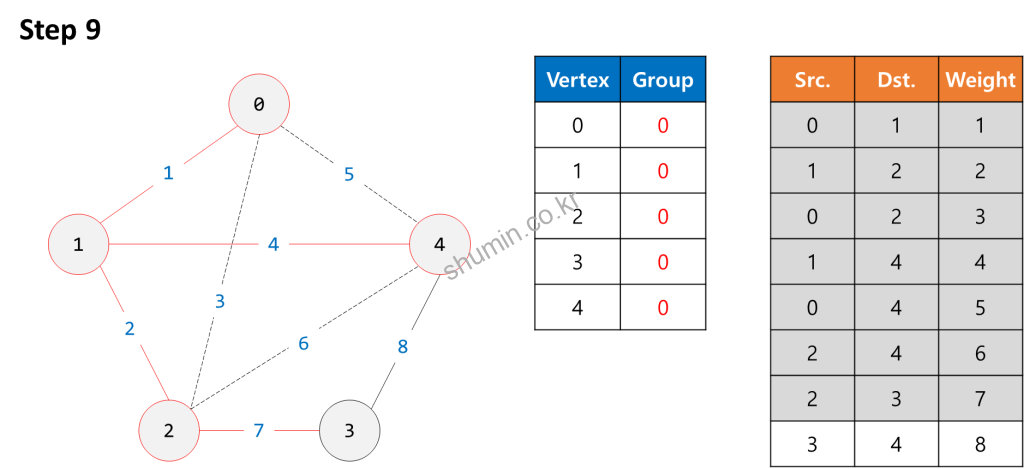
Source Code

#include <iostream>
#include <vector>
#include <algorithm>

#define NUM_EDGES 8
#define NUM_VERTEX 5

using namespace std;

class Edge
{
public:
    Edge(int _src, int _dst, int _w): src(_src), dst(_dst), w(_w) {}
    int src;
    int dst;
    int w;
};

vector<Edge> edge_list;
int group_table[NUM_VERTEX];
int total_weight;

bool cmp(Edge e1, Edge e2)
{
    if (e1.w == e2.w)
        return e1.src < e2.src;
    else
        return e1.w < e2.w;
}

void addEdge(int _s, int _d, int _w, int _bidirection)
{
    edge_list.push_back(Edge(_s, _d, _w));
}

void updateGroupTable(int _s, int _d)
{
    int s_group = group_table[_s];
    int d_group = group_table[_d];
    int smaller = (s_group < d_group) ? s_group : d_group;
    int bigger = (s_group < d_group) ? d_group : s_group;

    for (int i=0; i<NUM_VERTEX; i++) {
        if (group_table[i] == bigger)
            group_table[i] = smaller;
    }
}

void doMST(void)
{
    int edge_num = 0;
    for (int i=0; i<NUM_EDGES; i++) {
        // Compare group number
        if (group_table[edge_list[i].src] != group_table[edge_list[i].dst]) {
            printf("[%d]---(%d)---[%d]\n", edge_list[i].src, edge_list[i].w, edge_list[i].dst);
            edge_num++;
            total_weight += edge_list[i].w;

            if (edge_num == NUM_VERTEX + 1) {
                return;
            }

            updateGroupTable(edge_list[i].src, edge_list[i].dst);
        }
    }
}

int main(void)
{
    for (int i=0; i<NUM_VERTEX; i++)
        group_table[i] = i;

    addEdge(0, 1, 1, true);
    addEdge(0, 2, 3, true);
    addEdge(0, 4, 5, true);
    addEdge(1, 2, 2, true);
    addEdge(1, 4, 4, true);
    addEdge(2, 4, 6, true);
    addEdge(2, 3, 7, true);
    addEdge(3, 4, 8, true);

    sort(edge_list.begin(), edge_list.end(), cmp);

    doMST();

    printf("Total weight: %d\n", total_weight);

    return 0;
}

 [0]---(1)---[1]
 [1]---(2)---[2]
 [1]---(4)---[4]
 [2]---(7)---[3]
Total weight: 14