[Algorithm] Hamming Weight (Bit Count)
Data에서 1의 개수를 세는 알고리즘을 Hamming Weight라고 부른다. 여기엔 다양한 알고리즘이 존재한다.
1. Simple
int bit_count(int bit) {
int count = 0;
while (bit > 0) {
count += bit & 0x1;
bit = bit >> 1;
}
return count;
}
위 방식의 시간복잡도는 O(n)을 가진다.
2. Hamming Weight: Level 1
#include <stdio.h>
const int m1 = 0x55555555;
const int m2 = 0x33333333;
const int m4 = 0x0f0f0f0f;
const int m8 = 0x00ff00ff;
const int m16 = 0x0000ffff;
int popcount_a(int x) {
x = (x & m1 ) + ((x >> 1) & m1 );
x = (x & m2 ) + ((x >> 2) & m2 );
x = (x & m4 ) + ((x >> 4) & m4 );
x = (x & m8 ) + ((x >> 8) & m8 );
x = (x & m16) + ((x >> 16) & m16);
return x;
}
int main() {
int bitmap = 0x12345678;
int count;
count = popcount_a(bitmap);
printf("count=%d\n", count );
return 0;
}
위 코드는 wikipedia에 나와있는 코드를 32-bit에 맞춰서 변경해봤다. 만약 우리가 0x12345678에 대해 hamming weight를 구한다고 가정 했을 때 어떻게 위 알고리즘이 동작하는지 아래에 설명한다.
우선 popcount_a() 함수의 x = (x & m1) + ((x >> 1) & m1); 부분부터 설명하자면 2-bit씩 짝을 지어 짝지은 1-bit씩 더하는 연산을 수행하게 된다.

위 값을 보면 Final Data를 토대로 Origin Data에서 어떻게 나온지 알 수 있는데, 2-bit 단위로 1의 개수를 세어 2진수로 결과가 Final Data에 기록이 된다. 1의 개수는 0 ~ 3개가 될 수 있으므로 총 2-bit로 표현이 가능하다. 이런 방식으로 계속해서 모든 숫자를 더하여 최종 32-bit까지 더해서 나온 하위 6-bit (0 ~ 63)의 값을 통해서 1의 개수를 셀 수 있다. 따라서 위 함수의 각 line별로 2-bit, 4-bit, 8-bit, 16-bit, 32-bit에 대한 1의 개수의 합을 구할 수 있다.
이 알고리즘의 단점은 너무 많은 연산이 들어가기 때문에 좀 더 효과적인 알고리즘이 나왔다.
2. Hamming Weight: Level 2
int popcount_b(int x) {
x -= (x >> 1) & m1;
x = (x & m2) + ((x >> 2) & m2);
x = (x + (x >> 4)) & m4;
x += x >> 8;
x += x >> 16;
return x & 0x7f;
}
위 코드는 우리가 앞서 본 Level 1 코드와 동일한 동작을 하는데, 각 line별로 단위 bi당 1의 개수를 구하는 방식이다.
2.1 2-bit sum
코드에 나온 방식대로 binary로 구해보면 아래와 같이 우리가 구한 값과 동일하게 00010001_00100100_01010101_01100100가 나타난다.

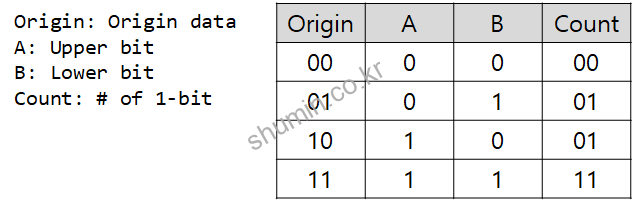
이유는 2-bit당 1-bit count의 값에 대해 truth table을 분석해보면, 1-bit shift right한 값은 A에 해당하는데, 위 표에서 보이듯이, A의 값을 original에서 빼면 count 값이 나오는 결과를 보이기 때문이다.
2.2 8-bit sum
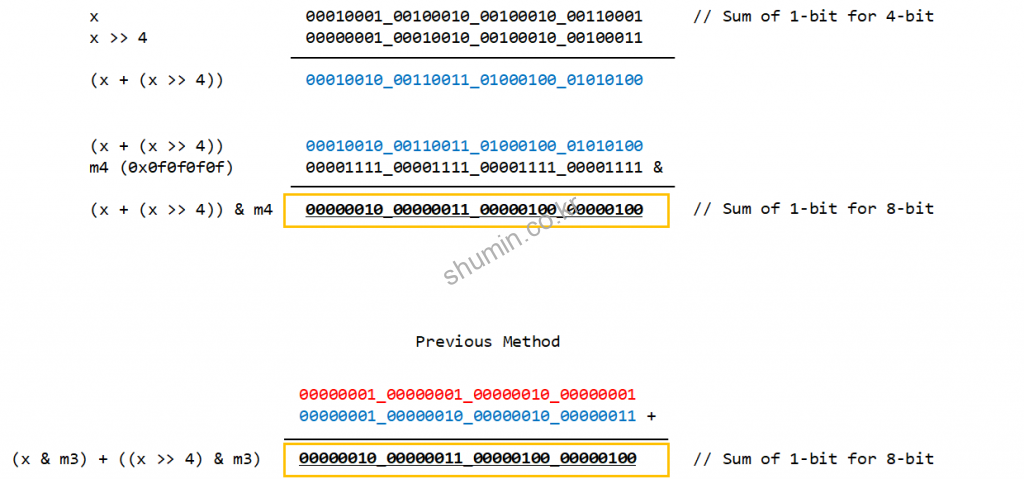
4-bit에 대한 1-bit count 방식은 동일하고, 8-bit의 경우엔 보면 약간 다른데, 기존엔 상위 4-bit masking한 값과 하위 4-bit masking한 값을 더했지만, 이번엔 따로 masking을 먼저 하지 않고 바로 상위 4-bit + 하위 4-bit을 수행시키고 난 뒤에 상위 4-bit에 대해서 모두 0으로 만들었다.
이렇게 해도 되는 이유는, 이미 4-bit count에 대한 값을 모두 더해도 4-bit으로 충분히 표현 할 수 있기 때문이다. (즉 overflow가 발생하지 않음)
2.3 16-bit & 32-bit sum

16-bit count는 8-bit count 방식과 비슷한데, masking을 하지 않고 중간 값을 바로 32-bit count를 구하는데 사용한다. 왜냐하면 어차피 32-bit count를 계산 할 때는 문제가 없고, 최종적으로 하위 bit masking을 하면 되기 때문이다. 이를 통해 불필요한 중간에 사용되는 연산을 제거 할 수 있다.
3. Hamming Weight: Level 3
const int h01 = 0x01010101;
int popcount_c(int x)
{
x -= (x >> 1) & m1;
x = (x & m2) + ((x >> 2) & m2);
x = (x + (x >> 4)) & m4;
return (x * h01) >> 24;
}
위 코드는 기존 Hamming Weight: Level 2 코드와 8-bit count 까지는 동일하고, 16-bit, 32-bit이 다르다.
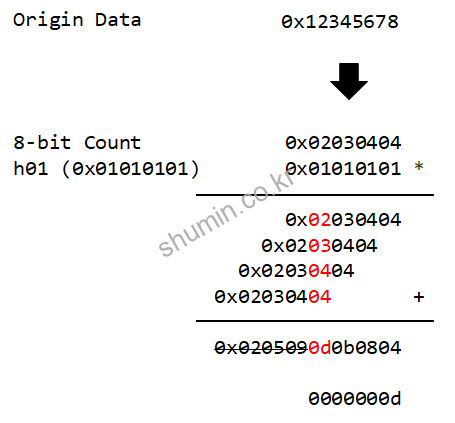
Level 3에선 곱셈의 성질을 이용했다. 일단 8-bit count를 세고 난 뒤 값에서 0x01010101를 곱한 결과에서, shift right를 통해 하위 24 bits을 제거한다. 이 의미는 result[31:24]인 상위 8-bit만 보겠다는 의미다. 참고로 32-bit data format이기 때문에 32-bit 이상 bit들은 무시된다.
요즘 CPU 내부에는 multiplier가 최적화가 잘 되어있기 때문에, 곱셈을 사용해도 성능이 좋다.
4. Hamming Weight: Level 4
int popcount_d(int x)
{
int count;
for (count=0; x; count++)
x &= x - 1;
return count;
}

위 알고리즘은 2진수의 특성을 이용해서 1의 개수를 세는 알고리즘이다. 우선 data에서 1을 뺀 값을 기존 data와 AND 연산을 수행해준다. 이렇게 될 경우 위 그림에서와 같이 count가 1로 증가하며, 1을 포함하는 하위 bit들이 모두 0으로 된다. 다음 iteration에도 동일하게 1을 뺀 결과를 기존의 값에서 빼면 다음 1이 있던 bit가 0으로 setting 된다.
이런 식으로 2진수의 특성을 이용해서 count를 하는데 이런 방식은 전체 data에서 1의 개수가 매우 적을 경우에만 사용한다. 기존 Level 3보다 이득이 되는 경우는 1의 개수가 log2n개 이하일 경우에만 사용하는게 유리하다. 32-bit data의 경우엔 5개 이하의 세팅 된 bit를 찾을 때는 유리하다.
Reference
- https://en.wikipedia.org/wiki/Hamming_weight