[Algorithm] Find First Set (FFS) Bit
FFS는 데이터 중에 특정 bit가 1로 설정됐는지 찾는 알고리즘이다.
#include <stdio.h>
int my_ffs(int bitmap) {
int i;
for(i=0; i<32; i++)
if(bitmap & (i<<i))
break;
return i;
}
int main() {
int bitmap = 0x01000000;
printf("%d\n", my_ffs(bitmap));
return 0;
}
위 코드는 하위 비트부터 순차적으로 for loop을 돌면서 무식하게 찾는 방법이다. 만약 찾고자 하는 bit가 상위에 있다면 시간이 오래 걸릴 것이다. (시간 복잡도는 O(n))
좀 더 효과적으로 찾는 알고리즘이 많은데, Linux Kernel에서 쓰이는 것을 소개한다.
#define BITS_PER_LONG 32
unsigned long __ffs(unsigned long word)
{
int num = 0;
#if BITS_PER_LONG == 64
if ((word & 0xffffffff) == 0) {
num += 32;
word >>= 32;
}
#endif
if ((word & 0xffff) == 0) {
num += 16;
word >>= 16;
}
if ((word & 0xff) == 0) {
num += 8;
word >>= 8;
}
if ((word & 0xf) == 0) {
num += 4;
word >>= 4;
}
if ((word & 0x3) == 0) {
num += 2;
word >>= 2;
}
if ((word & 0x1) == 0)
num += 1;
return num;
}

처음 if ((word & 0xffff) == 0)문은 하위 16 bits에 1이 없는지를 확인한다. 만약 하위 16 bits에 1이 하나도 없다면 16보다 큰 index에 1이 있을 수 있다. 만약 하위 16 bits에 0이 없다면 num은 16이 된다.

다음 동작은, 이전에 비교한 하위 16 bits 다음의 하위 8 bits를 masking 하여 0이 있는지를 검출한다. 만약 이번에도 없다면 num에 8을 더해준다.

다음 하위 4 bits를 비교해보니 이번엔 1이 검출이 되어 if문을 수행하지 않고 넘어간다.

그리고 다음 하위 2 bits를 비교하는 부분과 1 bit을 비교하는 부분도 모두 해당하지 않기 때문에 num은 24로 종료된다. 우리가 기대한 24가 나오는 것을 볼 수 있는데 이 알고리즘의 시간 복잡도는 O(log2n)이 된다.
그러나 이 알고리즘의 큰 단점이 있는데, 만약 찾고자 하는 단어가10000000_00000000_00000000_00000000 (0x8000)이라고 했을 때, 위 알고리즘은 최상단 bit이 1이 아니여도 동일한 결과를 나타낸다. 따라서 이런 경우를 방지하기 위해 bitmap이 0이 아닐 때만 검색하도록 확인을 하고 수행해야 한다.
int main()
{
unsigned long bitmap = 0x80000000UL;
if( bitmap != 0 )
printf("%lu\n", __ffs(bitmap));
else
printf("There is no 1 bit\n");
return 0;
}
확장 Bit Map
만약 64-bit을 넘어가는 경우에도 bit setting을 해야 할 수도 있다. 이 때는 확장 bit map을 구현해야 한다.

위 그림처럼 32-bit data를 4개를 사용해서 128-bit bit map을 구현하는데, 만약 111번째 bit setting을 하려고 할 때 shift operation (<<)를 사용하지 못한다. 따라서 다음과 같이 C 언어로 표현 할 수 있다.
int bitmap[4] = {0,};
// bitmap[3] |= 1 << 15;
bitmap[100/32] |= 1 << (111%32);
Find Nest Bit
만약 위 bit map을 바탕으로 process의 종류 별 priority를 넣어 관리한다고 한다. 숫자가 낮으면 낮을 수록 높은 priority를 가진다고 가정하고, 임의로 host process와 guest process로 나눈다고 하자. 그리고 사용하지 않는 영역을 reserved 영역이라고 하자.
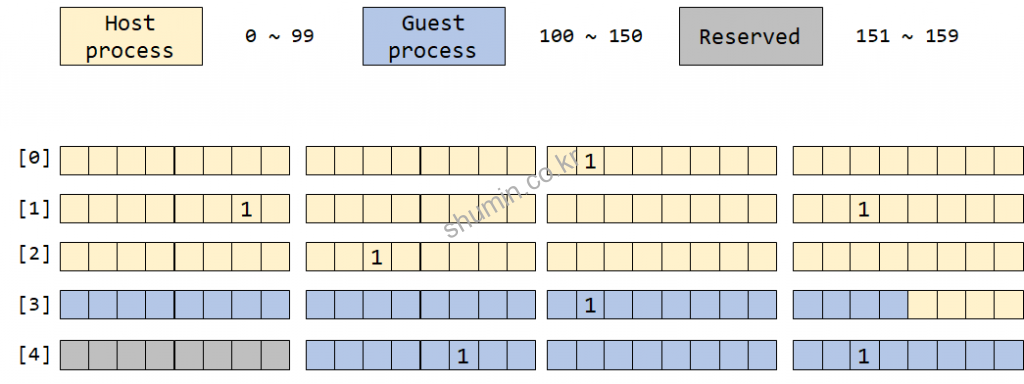
이런 구조에선 부분 별 bit map search가 되어야 한다. Kernel에선 이런 경우를 위한 함수를 지원하게 되는데 함수의 이름은 find_next_bit()으로 사용 방법은 다음과 같다.
int find_next_bit([bit map data, valid data size, start index);
위 함수의 return으로 우리가 찾고자 하는 구간에서 가장 우선순위가 높은 index가 나온다. find_next_bit의 함수는 아래와 같이 구현되어있다. 참고로 내부적으로 __ffs함수를 호출하기 때문에 이 함수도 넣어줘야 한다.
#define BITS_PER_LONG 64
#define BITOP_WORD(nr) ((nr) / BITS_PER_LONG)
unsigned long find_next_bit(const unsigned long *addr, unsigned long size,
unsigned long offset)
{
const unsigned long *p = addr + BITOP_WORD(offset);
unsigned long result = offset & ~(BITS_PER_LONG-1);
unsigned long tmp;
if (offset >= size)
return size;
size -= result;
offset %= BITS_PER_LONG;
if (offset) {
tmp = *(p++);
tmp &= (~0UL << offset);
if (size < BITS_PER_LONG)
goto found_first;
if (tmp)
goto found_middle;
size -= BITS_PER_LONG;
result += BITS_PER_LONG;
}
while (size & ~(BITS_PER_LONG-1)) {
if ((tmp = *(p++)))
goto found_middle;
result += BITS_PER_LONG;
size -= BITS_PER_LONG;
}
if (!size)
return result;
tmp = *p;
found_first:
tmp &= (~0UL >> (BITS_PER_LONG - size));
if (tmp == 0UL) /* Are any bits set? */
return result + size; /* Nope. */
found_middle:
return result + __ffs(tmp);
}
위 함수에 대한 분석은 추후에 진행이 필요할 것 같다. 생각보다 많이 복잡하다.
처음 BITOP_WORD 매크로는 bit map index를 구하여 우리가 찾고자 하는 pointer를 가져온다. 그리고 result는 우리가 사용하는 data type의 단위 (위 코드에선 64-bit)로 offset 값을 내림 한 결과를 보여준다. 보면 하위 bit들에 대해서 모두 0으로 만든다.