Algorithm,  Study

[Algorithm] Dijkstra Algorithm

February 12, 2023 /

Dijkstra algorithm은 한 점 (vertex)에서 모든 점까지 최단거리를 구하는 알고리즘이다. 자료구조에서는 graph 이론을 배우면서 반드시 알아야 할 내용이다. 각 vertex까지 최단거리를 구하는 과정은 다음과 같다.

  1. 초기화: 아직 방문하지 않는 vertex에 대해서는 거리는 무한대, 방문 정보는 false로 초기에 설정
  2. 처음 시작 vertex를 설정하고, table에서 방문 정보를 true로 설정
  3. 출발 vertex를 기준으로 연결된 vertex의 거리 정보를 업데이트
  4. 방문하지 않은 vertex 중 거리가 가까운 vertex부터 선택해 만약 거리가 더 가까운 경우 table 업데이트
  5. 모든 vertex를 방문했을 때 종료

Example

우선 위와 같은 graph가 있다고 가정하고, vertex 1부터 시작한다고 하자.

그리고 연결된 노드 정보를 table에 업데이트 해주고, 가장 가까운 노드인 vertex 4부터 방문한다.

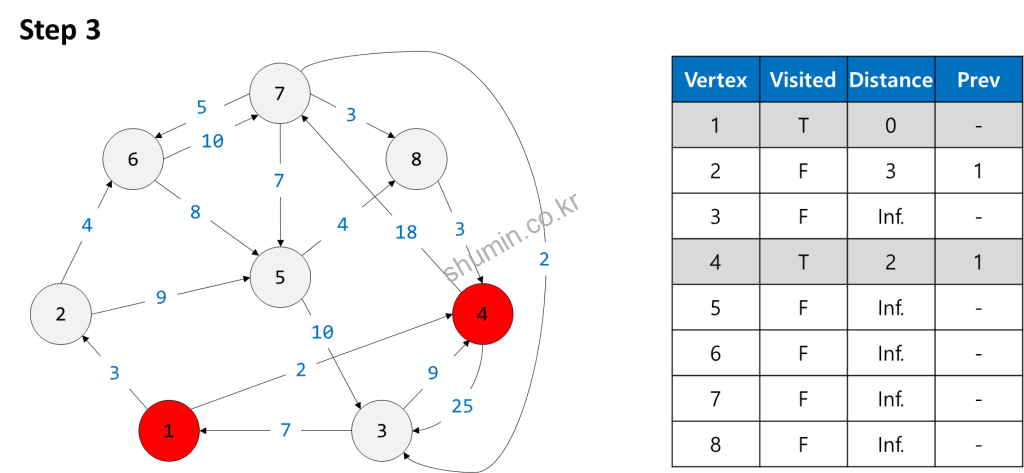
이제 vertex 3, 7을 업데이트 해준 뒤에, 출발 노드 기준으로 다음 가까운 vertex 2를 방문하도록 한다.

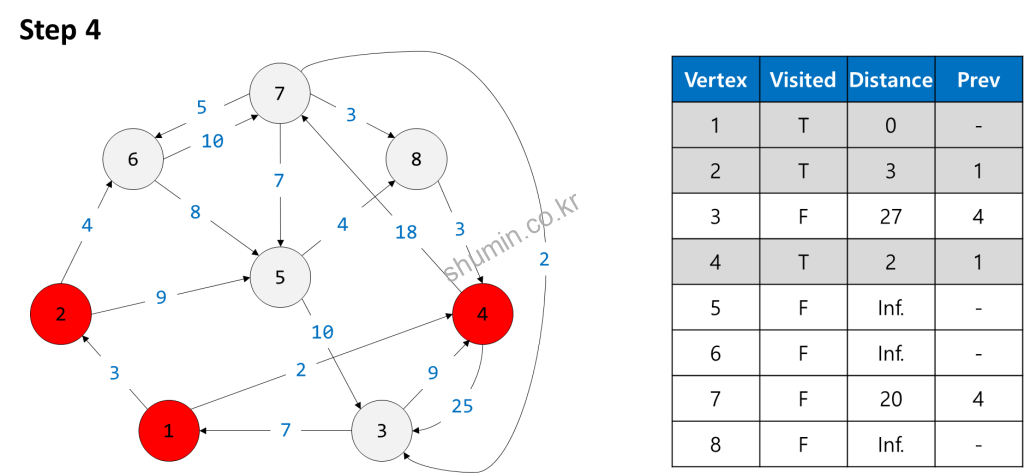
거리 정보를 업데이트 할 때 중요한 점은, 이전 노드의 거리 정보를 함께 더해줘야 한다. Vertex 2와 연결된 vertex 5, 6에 대해서 다시 table을 업데이트 해주고 나면 다음으로 짧은 vertex 6을 방문해준다.

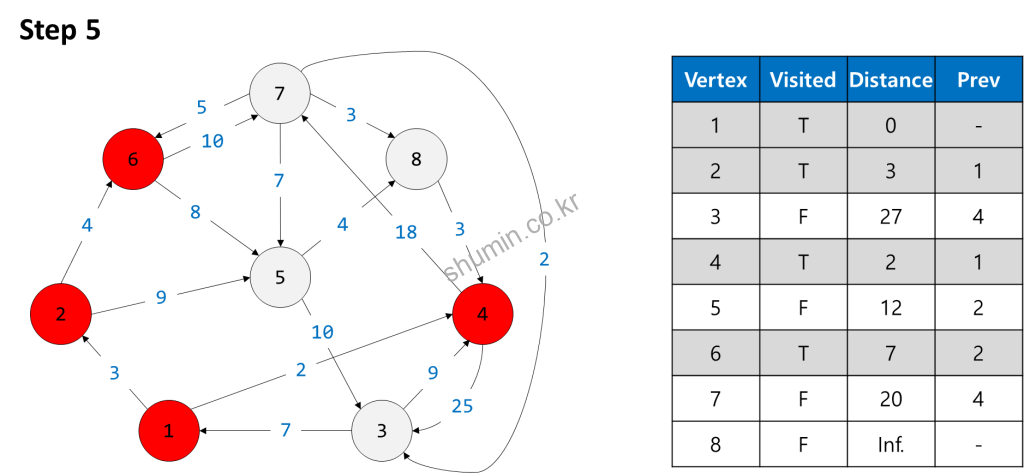
계속해서 새로 방문한 vertex 6에서 이동 가능한 vertex 5, 7을 업데이트 해주게 되는데 이미 방문한 vertex의 경우엔 기존에 기록된 거리값과 비교하여 작은 경로의 거리로 업데이트를 해주게 된다. 위 예시의 경우 vertex 7는 기존 경로는 20, 새롭게 방문된 경로는 17이기 때문에 새로운 경로의 정보로 업데이트 해준다.
그리고 다음 가까운 노드인 vertex 5를 방문한다.

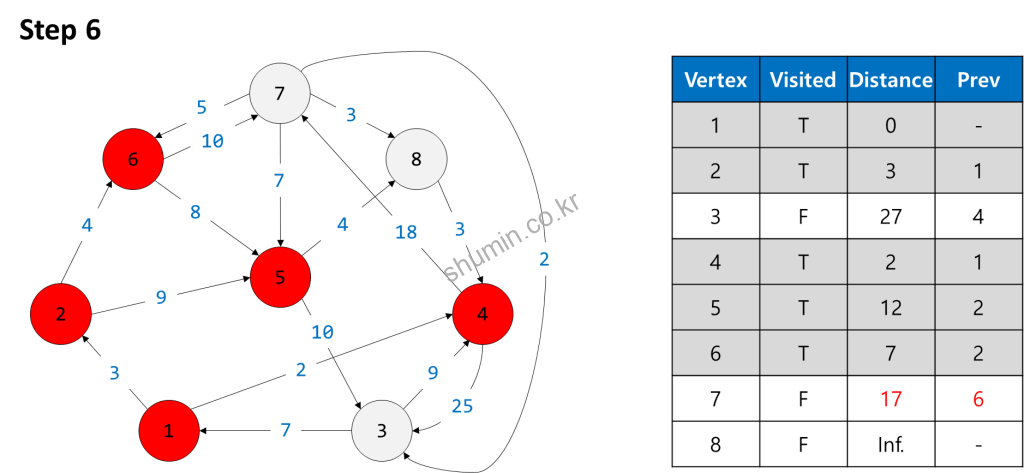
이제 vertex 5에서 3, 8을 연결이 가능한데, vertex 3의 경우에도 새롭게 방문된 경로 길이가 더 짧기 때문에 새롭게 업데이트를 해주고, 다음 짧은 경로인 vertex 8을 방문해준다.

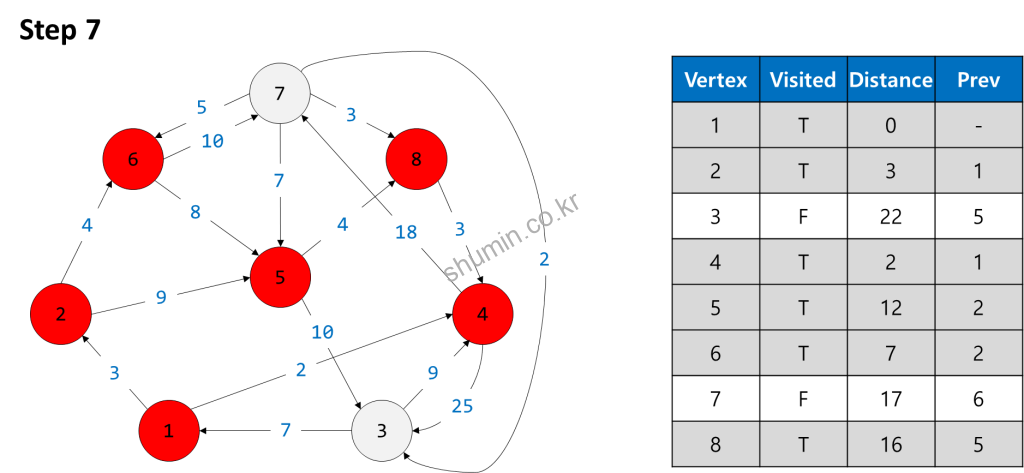
이제 다음 짧은 vertex 7을 방문해주고 이후에 vertex 3을 방문해주면 모든 vertex를 방문했기 때문에 탐색이 종료된다.

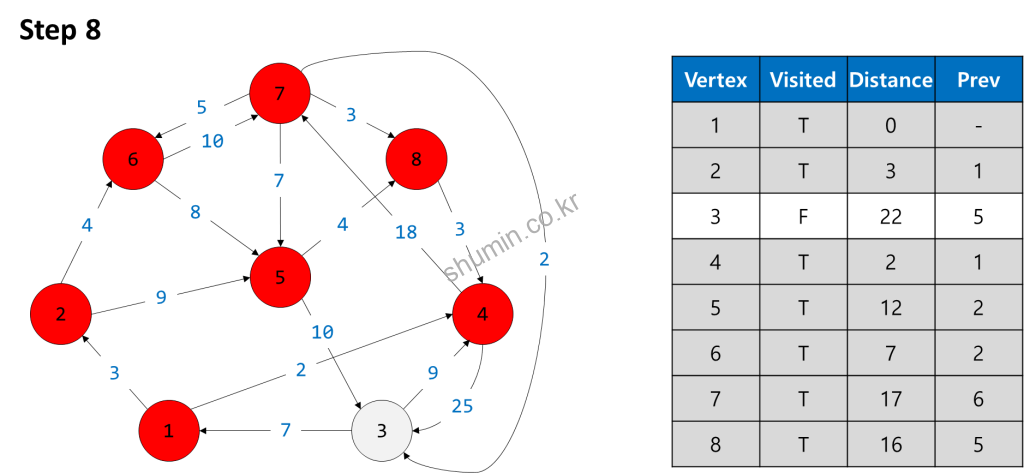
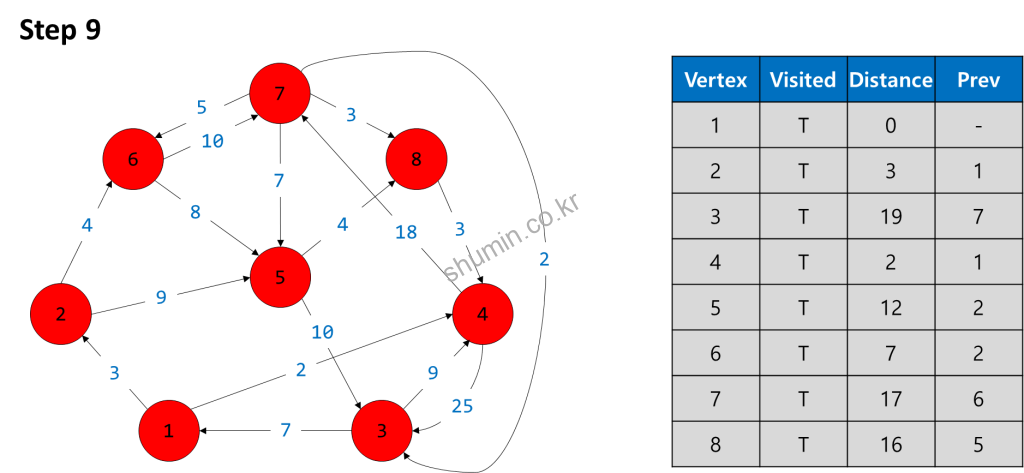
C++ Source Code (Linked-List Version)

#include <iostream>
#define NUM_VERTEX 8+1
#define MAX_W 9999999

using namespace std;

class Node
{
public:
    Node(int _v, int _w, Node *_next): v(_v), w(_w), next(_next) {}
    int v;
    int w;
    Node *next;
};

class Dijkstra
{
public:
    Dijkstra(): visited(false), w(0), prev(0) {}
    bool visited;
    int w;
    int prev;
};

Node *graph[NUM_VERTEX];
Dijkstra dtable[NUM_VERTEX];

void initDtable(void)
{
    for (int i=0; i<NUM_VERTEX; i++) {
        dtable[i].visited = false;
        dtable[i].w = MAX_W;
        dtable[i].prev = -1;
    }
}

void updateDtable(int v)
{
    Node *cur = graph[v];

    while(cur != nullptr) {
        if (!dtable[cur->v].visited && (dtable[cur->v].w > dtable[v].w + cur->w)) {
            dtable[cur->v].w = dtable[v].w + cur->w;
            dtable[cur->v].prev = v;
        }

        cur = cur->next;
    }
}

int findDijkstraNextV(void)
{
    int smallest_w = MAX_W;
    int smallest_v = -1;

    for (int i=1; i<=NUM_VERTEX; i++) {
        if (!dtable[i].visited && dtable[i].w < smallest_w) {
            smallest_w = dtable[i].w;
            smallest_v = i;
        }
    }

    return smallest_v;
}
void showDtable(void)
{
    for (int i=1; i<NUM_VERTEX; i++) {
        printf("%d: %d %d %d\n", i, dtable[i].visited, dtable[i].w, dtable[i].prev);
    }
}

void doDijkstra(int v)
{
    int next_v = -1;
    dtable[v].w = 0;

    while((next_v = findDijkstraNextV()) != -1) {
        dtable[next_v].visited = true;
        updateDtable(next_v);
    }

    showDtable();
}

void addEdge(int src, int dst, int w, bool bidirection)
{
    Node *new_node = new Node(dst, w, nullptr);
    Node *cur = graph[src];

    if (cur == nullptr) {
        graph[src] = new_node;
    } else {
        while(cur->next != nullptr) {
            cur = cur->next;
        }

        cur->next = new_node;
    }

    if (bidirection) {
        addEdge(dst, src, w, false);
    }
}
int main()
{
    addEdge(1, 2, 3, false);
    addEdge(1, 4, 2, false);
    addEdge(2, 5, 9, false);
    addEdge(2, 6, 4, false);
    addEdge(3, 1, 7, false);
    addEdge(3, 4, 9, false);
    addEdge(4, 3, 25, false);
    addEdge(4, 7, 18, false);
    addEdge(5, 3, 10, false);
    addEdge(5, 8, 4, false);
    addEdge(6, 5, 8, false);
    addEdge(6, 7, 10, false);
    addEdge(7, 5, 7, false);
    addEdge(7, 6, 5, false);
    addEdge(7, 8, 3, false);
    addEdge(7, 3, 2, false);
    addEdge(8, 4, 3, false);

    initDtable();

    doDijkstra(1);

    return 0;
}
$ ./a.out
1: 1 0 -1
2: 1 3 1
3: 1 19 7
4: 1 2 1
5: 1 12 2
6: 1 7 2
7: 1 17 6
8: 1 16 5

C++ Source Code (Array Version)

#include <iostream>
#define NUM_VERTEX 8+1
#define MAX_W 9999999

using namespace std;

class Dijkstra
{
public:
    Dijkstra(): visited(false), w(0), prev(0) {}
    bool visited;
    int w;
    int prev;
};

int graph[NUM_VERTEX][NUM_VERTEX];
Dijkstra dtable[NUM_VERTEX];

void initDtable(void)
{
    for (int i=0; i<NUM_VERTEX; i++) {
        dtable[i].visited = false;
        dtable[i].w = MAX_W;
        dtable[i].prev = -1;
    }
}

void updateDtable(int v)
{
    for (int i=1; i<NUM_VERTEX; i++) {
        if (graph[v][i] > 0) {
            if (!dtable[i].visited && (dtable[i].w > dtable[v].w + graph[v][i])) {
                dtable[i].w = dtable[v].w + graph[v][i];
                dtable[i].prev = v;
            }
        }
    }
}

int findDijkstraNextV(void)
{
    int smallest_w = MAX_W;
    int smallest_v = -1;

    for (int i=1; i<=NUM_VERTEX; i++) {
        if (!dtable[i].visited && dtable[i].w < smallest_w) {
            smallest_w = dtable[i].w;
            smallest_v = i;
        }
    }

    return smallest_v;
}

void showDtable(void)
{
    for (int i=1; i<NUM_VERTEX; i++) {
        printf("%d: %d %d %d\n", i, dtable[i].visited, dtable[i].w, dtable[i].prev);
    }
}
void doDijkstra(int v)
{
    int next_v = -1;
    dtable[v].w = 0;

    while((next_v = findDijkstraNextV()) != -1) {
        dtable[next_v].visited = true;
        updateDtable(next_v);
    }

    showDtable();
}

void addEdge(int src, int dst, int w, bool bidirection)
{
    graph[src][dst] = w;

    if (bidirection) {
        graph[dst][src] = w;
    }
}

int main()
{
    addEdge(1, 2, 3, false);
    addEdge(1, 4, 2, false);
    addEdge(2, 5, 9, false);
    addEdge(2, 6, 4, false);
    addEdge(3, 1, 7, false);
    addEdge(3, 4, 9, false);
    addEdge(4, 3, 25, false);
    addEdge(4, 7, 18, false);
    addEdge(5, 3, 10, false);
    addEdge(5, 8, 4, false);
    addEdge(6, 5, 8, false);
    addEdge(6, 7, 10, false);
    addEdge(7, 5, 7, false);
    addEdge(7, 6, 5, false);
    addEdge(7, 8, 3, false);
    addEdge(7, 3, 2, false);
    addEdge(8, 4, 3, false);

    initDtable();

    doDijkstra(1);

    return 0;
}

C++ Source Code (Priority Queue Version)

기존 코드의 시간복잡도를 계산해보면 O(N^2)으로 나타낼 수 있다. 이유는 다음 두 개의 loop을 가지기 때문이다.

  • 시작 노드를 기준으로 가장 짧은 거리를 가지는 vertex를 찾는 과정
  • 가장 짧은 노드를 기준으로 연결된 노드 중 방문하지 않았으며, 기존 계산된 거리보다 짧은 노드를 찾는 과정

위 두 단계의 loop으로 인해 시간 복잡도는 꽤 높게 나타난다. 이를 극복하기 위해 사용되는 방식이 priority queue를 사용하는 방식이다.

Priority queue를 사용해 가장 짧은 거리를 가지는 vertex를 찾는 과정을 시작 노드 기준으로 모두 접근하지 않고, priority queue의 top의 정보만으로 쉽게 next vertex를 얻을 수 있다.

아래는 예시 코드다.

#include <iostream>
#include <queue>
#define NUM_VERTEX 8+1
#define MAX_W 9999999

using namespace std;

class Dijkstra
{
public:
    Dijkstra(): visited(false), w(0), prev(0) {}
    bool visited;
    int w;
    int prev;
};

int graph[NUM_VERTEX][NUM_VERTEX];
int dtable[NUM_VERTEX];
priority_queue<pair<int, int>> pq;

void initDtable(void)
{
    for (int i=0; i<NUM_VERTEX; i++) {
        dtable[i] = MAX_W;
    }
}

void updateDtable(int v)
{
    for (int i=1; i<NUM_VERTEX; i++) {
        if (graph[v][i] > 0) {
            if (dtable[i] > dtable[v] + graph[v][i]) {
                dtable[i] = dtable[v] + graph[v][i];
                pq.push(make_pair(dtable[i], i));
            }
        }
    }
}

void showDtable(void)
{
    for (int i=1; i<NUM_VERTEX; i++) {
        printf("%d: %d\n", i, dtable[i]);
    }
}

void doDijkstra(int v)
{
    pq.push({0, v});
    dtable[v] = 0;

    while(!pq.empty()) {
        int dist = pq.top().first;
        int next_v = pq.top().second;
        pq.pop();

        if (dtable[next_v] < dist)
            continue;

        updateDtable(next_v);
    }

    showDtable();
}
void addEdge(int src, int dst, int w, bool bidirection)
{
    graph[src][dst] = w;

    if (bidirection) {
        graph[dst][src] = w;
    }
}

int main()
{
    addEdge(1, 2, 3, false);
    addEdge(1, 4, 2, false);
    addEdge(2, 5, 9, false);
    addEdge(2, 6, 4, false);
    addEdge(3, 1, 7, false);
    addEdge(3, 4, 9, false);
    addEdge(4, 3, 25, false);
    addEdge(4, 7, 18, false);
    addEdge(5, 3, 10, false);
    addEdge(5, 8, 4, false);
    addEdge(6, 5, 8, false);
    addEdge(6, 7, 10, false);
    addEdge(7, 5, 7, false);
    addEdge(7, 6, 5, false);
    addEdge(7, 8, 3, false);
    addEdge(7, 3, 2, false);
    addEdge(8, 4, 3, false);

    initDtable();

    doDijkstra(1);

    return 0;
}
$ ./a.out
1: 0
2: 3
3: 19
4: 2
5: 12
6: 7
7: 17
8: 16

Leave a Reply

Your email address will not be published. Required fields are marked *