[Algorithm] Cyclic Redundancy Check (CRC)
Check Sum의 문제는 data의 합이 변하지 않으면, 중간에 data들이 변하여도 error를 찾을 수 없는 문제가 있다. 따라서 이런 문제를 해결할 수 있는 방식이 CRC다.
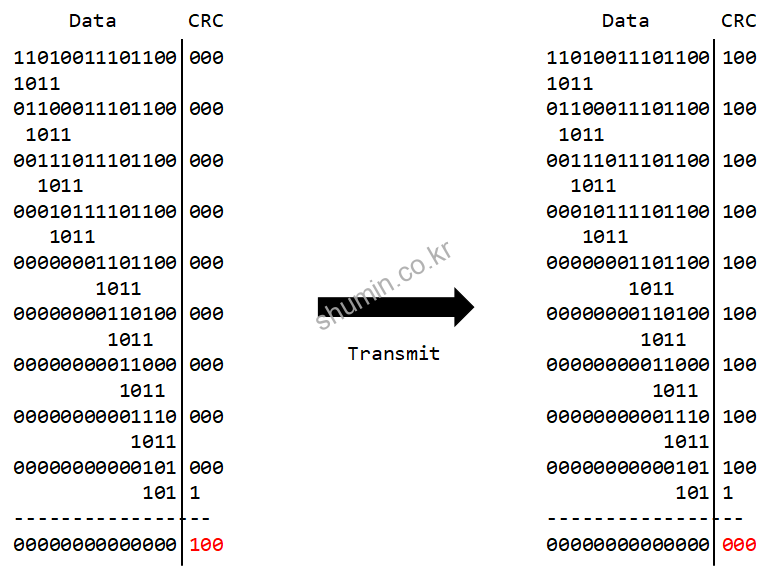
위 그림은 3-bit CRC의 예시로, 보내는 sender쪽에서 data를 특정 divisor (1011)과 XOR를 해서 나온 결과를 다시 recursive하게 진행한다.
최종적으로 모든 data가 0으로 됐을 때, 하위에 잔여 data가 CRC값으로, data와 함께 전송시켜서 receiver에서 동일한 방식으로 CRC 값을 확인해서 0이 나오면 올바른 data가 된다.
8-bit CRC

Data: 0x14
Divisor: 0x1D5
CRC: 0xAC
8-bit CRC 예시를 위와 같이 보였다. 실제로 8-bit CRC (10101100)의 값을 전달해서 Receiver쪽에서 CRC function을 수행하면 모든 값이 0으로 나오는 것을 볼 수 있다. 참고로 divisor의 값은 이미 정해져있다. (Wikipedia를 참고하면 된다.)
만약 다음 data가 0x52라고 했을 때, 이전에 나온 CRC 값과 다음 보낼 data인 0x52와 XOR한 값을 CRC 함수에 넣어줘야 한다.
Next CRC = CRC (Current CRC ^ Next Data)Next CRC = CRC (0xAC ^ 0x52)
CRC는 중간에 data가 하나라도 변할 경우에 뒤에 data는 계속해서 error가 발생할 것이다.
실제 Linux Kernel에서도 CRC를 사용하는데, CRC 함수를 호출하지 않고 CRC table을 미리 만들어 lookup table로 사용한다. 실제 코드를 활용한 예시 코드는 아래와 같다.
#include <stdio.h>
typedef unsigned char u8;
#define CRC8_TABLE_SIZE 256
void crc8_populate_msb(u8 *table, u8 polynomial)
{
int i, j;
const u8 msbit = 0x80;
u8 t = msbit;
table[0] = 0;
for (i = 1; i < CRC8_TABLE_SIZE; i *= 2) {
t = (t << 1) ^ (t & msbit ? polynomial : 0);
for (j = 0; j < i; j++)
table[i+j] = table[j] ^ t;
}
}
u8 crc8( u8 *table, u8 *pdata, size_t nbytes, u8 crc)
{
while (nbytes-- > 0)
crc = table[(crc ^ *pdata++) & 0xff];
return crc;
}
u8 table[CRC8_TABLE_SIZE];
void display( u8 *table )
{
int i;
for( i=0; i<256; i++ )
{
printf("%02x ", table[i] );
if( (i+1)%16 == 0 )
printf("\n");
}
}
int main()
{
u8 data[3] = {0x14, 0x52, 0 };
u8 crc = 0x0;
crc8_populate_msb(table, 0xd5);
display( table );
crc = crc8( table, data, 2, 0 );
printf("crc=%#x\n", crc );
data[2] = crc;
data[0]++;
data[1]--;
//============================================
crc = crc8( table, data, 3, 0 );
if( crc == 0 )
printf("Data is valid\n");
else
printf("Data is invalid\n");
return 0;
}
00 d5 7f aa fe 2b 81 54 29 fc 56 83 d7 02 a8 7d 52 87 2d f8 ac 79 d3 06 7b ae 04 d1 85 50 fa 2f a4 71 db 0e 5a 8f 25 f0 8d 58 f2 27 73 a6 0c d9 f6 23 89 5c 08 dd 77 a2 df 0a a0 75 21 f4 5e 8b 9d 48 e2 37 63 b6 1c c9 b4 61 cb 1e 4a 9f 35 e0 cf 1a b0 65 31 e4 4e 9b e6 33 99 4c 18 cd 67 b2 39 ec 46 93 c7 12 b8 6d 10 c5 6f ba ee 3b 91 44 6b be 14 c1 95 40 ea 3f 42 97 3d e8 bc 69 c3 16 ef 3a 90 45 11 c4 6e bb c6 13 b9 6c 38 ed 47 92 bd 68 c2 17 43 96 3c e9 94 41 eb 3e 6a bf 15 c0 4b 9e 34 e1 b5 60 ca 1f 62 b7 1d c8 9c 49 e3 36 19 cc 66 b3 e7 32 98 4d 30 e5 4f 9a ce 1b b1 64 72 a7 0d d8 8c 59 f3 26 5b 8e 24 f1 a5 70 da 0f 20 f5 5f 8a de 0b a1 74 09 dc 76 a3 f7 22 88 5d d6 03 a9 7c 28 fd 57 82 ff 2a 80 55 01 d4 7e ab 84 51 fb 2e 7a af 05 d0 ad 78 d2 07 53 86 2c f9 crc=0x2c Data is invalid
Reference
- https://en.wikipedia.org/wiki/Cyclic_redundancy_check