[Algorithm] Pattern Matching
패턴매칭은 우리가 평소에 작업을 할 때 많이 사용한다. 예를 들면 strstr() 함수라던지 vim에서 / 동작, word에서 Ctrl+F 등 많은 utility에서 사용되고 있다. 패턴 매칭을 위해서 많은 loop을 돌아야하기 때문에 시간 복잡도는 O(n*m)이 된다. n은 본문의 문자열 길이, m은 찾고자 하는 단어 길이다.
x: 찾는 문자열m: 찾는 문자열 길이y: 본문 문자열n: 본문 문자열 길
Kernel에서도 많은 pattern matching 알고리즘이 많이 사용된다. 지금부터 유명한 pattern matching 알고리즘을 소개한다.
Brute Force
void BF(char *x, int m, char *y, int n) {
int i, j;
// Search
for (j=0; j<=n-m; j++) {
for (i=0; i<m && x[i] == y[i+j]; i++);
if (i>=m)
OUTPUT(j);
}
}
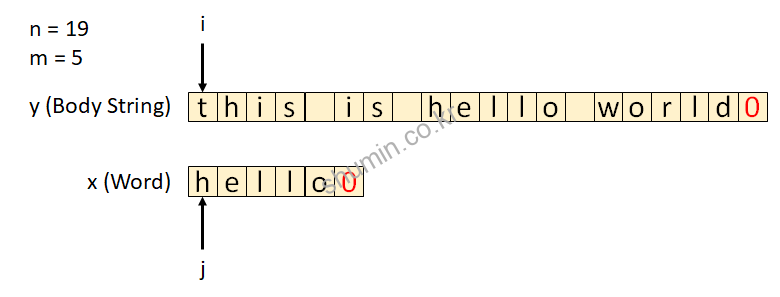
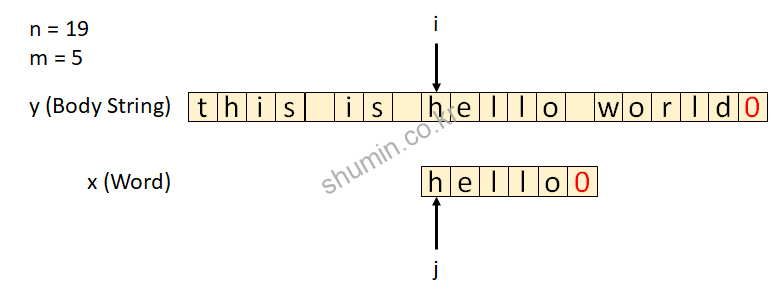
내부 코드를 보면 for loop이 2개가 있는데, 바깥쪽 loop은 본문 문자열을 도는 loop, 안쪽 loop은 찾고자 하는 문자열 길이만큼 돌도록 되어있는데, 매치되는 단어 개수만큼 다 돌아야지 최종적으로 pattern이 일치한다는 결과를 출력한다. if (i>=m) 조건을 만족할 때 우리가 찾고자 하는 pattern이 존재하는지 확인되는 부분이다.
실제 Brute Force 알고리즘으로 strstr() 함수가 짜여있는데, 이보다 더 나은 성능을 가지는 패턴 매칭 알고리즘이 존재한다.
Karp-Rabin
#define REHASH(a, b, h) ((((h) - (a)*d) << 1) + (b))
void KR(char *x, int m, char *y, int n) {
int d, hx, hy, i, j;
/* Preprocessing */
/* computes d = 2^(m-1) with
the left-shift operator */
for (d = i = 1; i < m; ++i)
d = (d<<1);
for (hy = hx = i = 0; i < m; ++i) {
hx = ((hx<<1) + x[i]);
hy = ((hy<<1) + y[i]);
}
/* Searching */
j = 0;
while (j <= n-m) {
if (hx == hy && memcmp(x, y + j, m) == 0)
OUTPUT(j);
hy = REHASH(y[j], y[j + m], hy);
++j;
}
}
함수 내부를 보면 hx와 hy는 hash를 의미한다.
우리는 찾고자 하는 문자열이 “hello”라고 가정하고 설명한다.
hx = ((hx<<1) + x[i])가 의미하는 것은, 자신의 값을 2를 곱하고 첫 번째 글자의 ASCII값을 더한 hash 값이다. 'h'부터 '\n'까지 recursive하게 수행한다. 해당 함수는 우리가 10진수 숫자를 쓰는 것처럼, 각 ASCII 값에 가중치를 주어서 더한 것이다. 따라서 본문을 비교하지 않고, hash 값을 비교하는 방법이다. 아래는 찾고자 하는 단어의 hash값을 구하는 순서다.
hx = 0*2 + ‘h’ hx = ‘h’*2 + ‘e’ hx = ‘h’*2^2 ‘e’*2^1 + ‘l’*2^0 hx = ‘h’*2^3 ‘e’*2^2 + ‘l’*2^1 + ‘l’*2^0 hx = ‘h’*2^4 ‘e’*2^3 + ‘l’*2^2 + ‘l’*2^1 + ‘o’*2^0
그런데 본문 문자열의 hash 값은 계속 바뀌게 될텐데, 매번 본문 문자열의 hash값을 새로 구하지 않고, 기존에 구한 것을 활용하기 위해 사용하는 함수가 REHASH()다. 매번 hash값을 구하는 것은 overhead가 되기 때문이다.

맨 앞에 ASCII 문자를 뺀 값을 2를 곱해주고, 새로운 ASCII 문자값을 더해준다.hy = (hy - y[j]*2^4) << 1) + y[j+m]
따라서 전체 시간복잡도는 O(n+m)가 된다.
Shift Or (SO)
Shift Or 알고리즘은 SO라고 부르기도 하는데, 내부는 크게 preSO 함수와 SO 함수로 나뉜다.
preSO
int preSo(char *x, int m, unsigned int S[]) {
unsigned int j, lim;
int i;
for (i = 0; i < ASIZE; ++i)
S[i] = ~0;
for (lim = i = 0, j = 1; i < m; ++i, j <<= 1) {
S[x[i]] &= ~j;
lim |= j;
}
lim = ~(lim>>1);
return(lim);
}
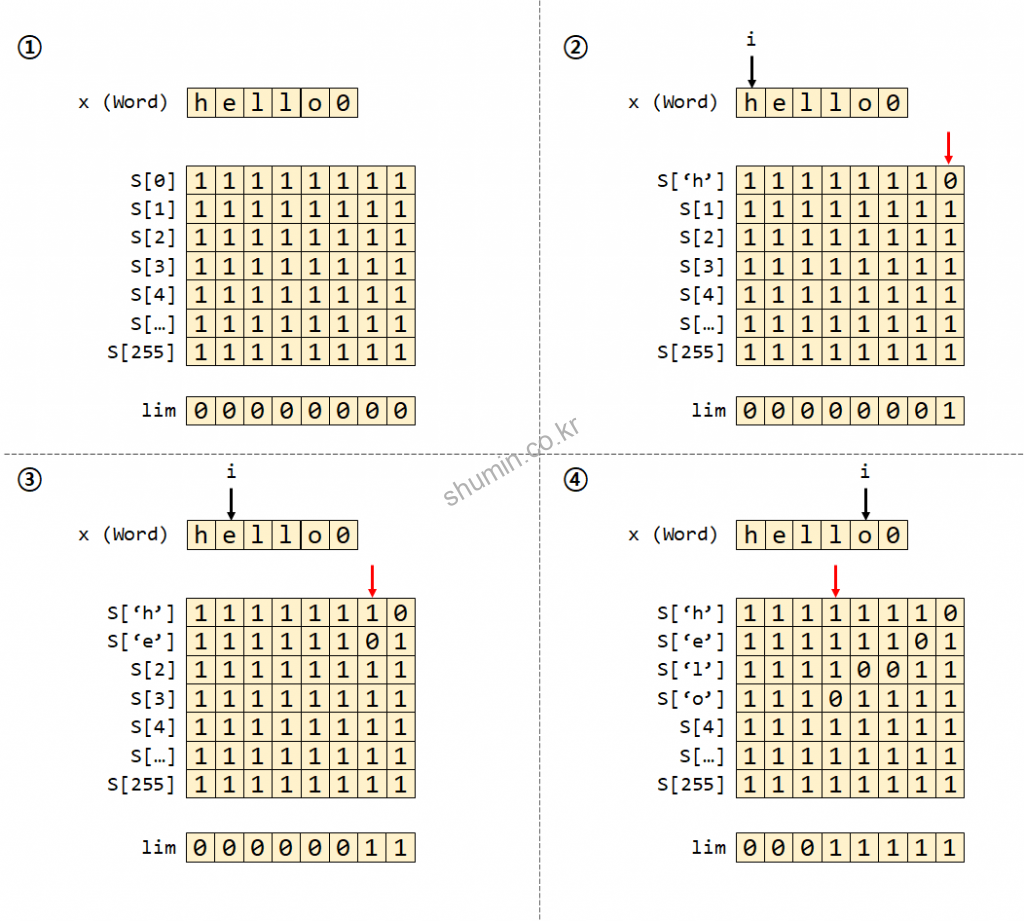
이 알고리즘은 처음에 lookup table을 만들고 시작한다. S라는 lookup table을 처음에 모두 1로 초기화한다. 참고로 S의 크기는 256으로, 모든 char 문자정보 (ASCII는 8-bit 정보)를 담기 위해서 256개를 가진다.
찾고자 하는 문자열의 첫 문자부터 순차적으로 lookup table에 ‘0’ 값으로 표시를 하고, lim 값에는 ‘0’으로 변경한다. 코드를 보면 연산은 shift 연산과 and, or 연산이 주로 사용되는데, 이를 통해 메모리 사용을 최소화할 수 있다.
SO
void SO(char *x, int m, char *y, int n) {
unsigned int lim, state;
unsigned int S[ASIZE];
int j;
// if (m > WORD)
// error("SO: Use pattern size <= word size");
/* Preprocessing */
lim = preSo(x, m, S);
/* Searching */
for (state = ~0, j = 0; j < n; ++j) {
state = (state<<1) | S[y[j]];
if (state < lim)
OUTPUT(j - m + 1);
}
}
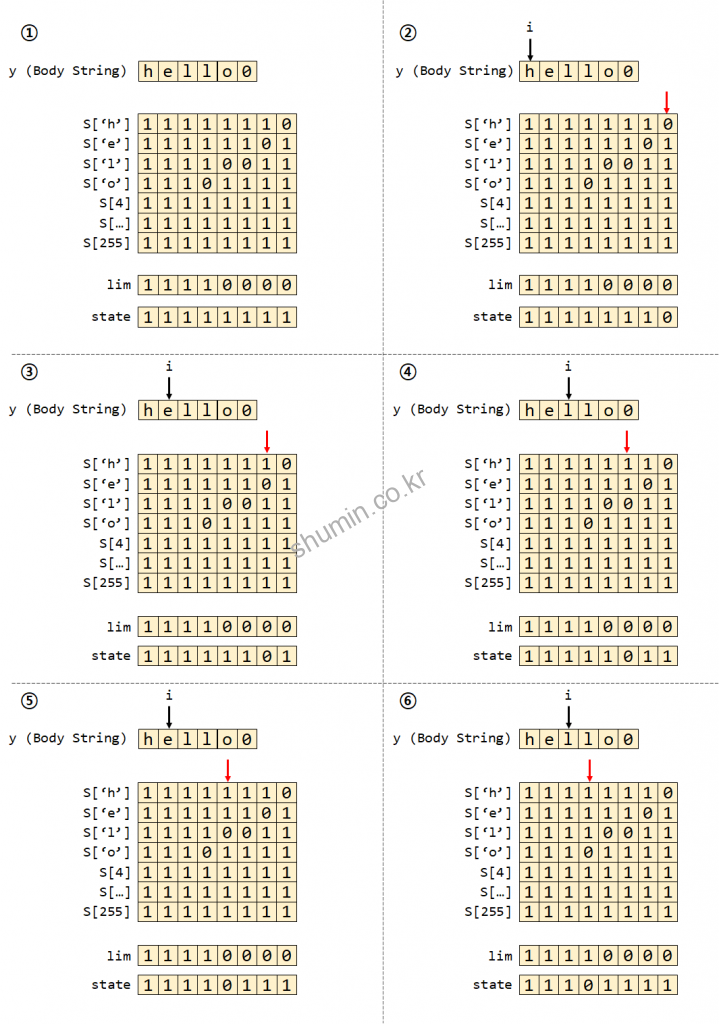
이제 우리가 만든 lookup table과 lim을 통해 패턴을 확인한다. 내부엔 state라는 변수가 추가로 사용되는데 처음에 모든 bit을 1로 초기화한다.
state = (state<<1) | S[y[j]]를 통해 본문의 문자열의 각 문자 ASCII값을 통해 lookup table로 접근해서state값을 업데이트해준다.- Shift 연산을 통해서 가장 하위 bit에 ‘0’을 생성하게 되는데, 만약 연속적으로 패턴이 일치할 경우에만 ‘0’이 상위 bit로 이동하는 모습이 생긴다. 만약 하나라도 틀리면
state에 생긴 ‘0’은 끝까지 상위 bit로 이동 할 수 없다. - 최종적으로
state의 ‘0’이 계속 상위 bit로 이동해서state가lim보다 작을 때 우리가 찾고자 하는 단어를 찾은 것이다.
Shift OR 알고리즘은 그러나 본문 문자열의 수만큼 모두 돌려야하는 복잡도 (O(m+n))를 가진다. 물론 Brute Force보다는 더 효과적이지만 여전히 불필요한 for loop이 필요하다.
Reference
- http://www-igm.univ-mlv.fr/~lecroq/string