증강 트리 (Augmented Tree)

소개

Augmented Tree (증강 트리)는 기존 binary search tree에서 확장된 구조다.

Binary search tree에서 이론상 특정 값을 검색 할 때, log2(N)만큼의 시간복잡도를 가지기 때문에 balance만 맞춰져 있다고 하면 빠르게 찾을 수 있다. 그러나 만약 “7번째로 큰 값은?” 이라는 주제에 대해선 빠르게 찾기 어렵기 때문에 증강 트리가 고안 되었다. 우선 예시 증강 트리 구조를 그려보면 아래와 같다. 증강 (augmented) 값은 데이터 값 아래에 적었다.

우선 증강 값은 가장 하위 노드는 항상 1이며, 부모 노드는 자식 노드들의 합에 1을 더한다. 그리고 찾고자 하는 몇 번째를 가리키는 index인 i 값과, 기준 값을 의미하는 k를 두는데, k는 항상 왼쪽 sub-tree의 augmented 값에 1을 더한 값이다.

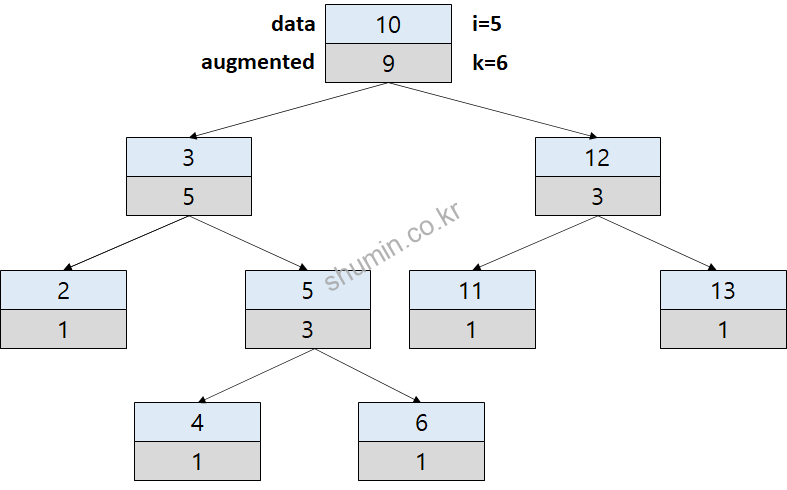
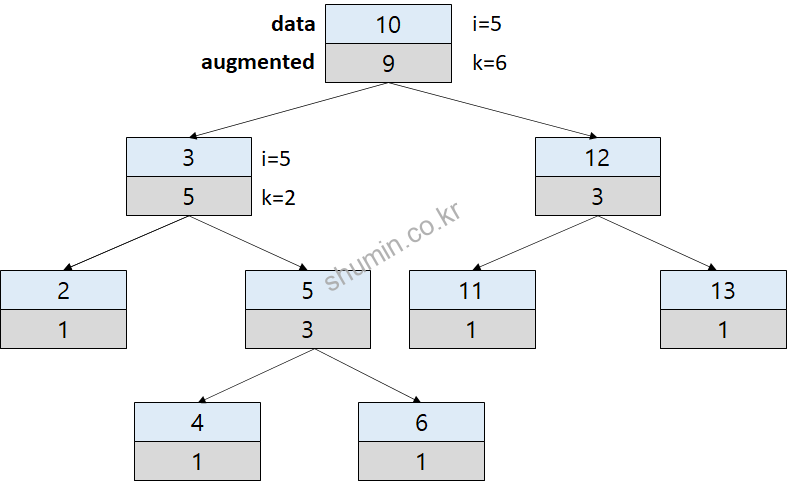
root 부터 traverse를 진행하게 되는데, 인덱스 값 (i)이 기준점 (k)보다 작으면 왼쪽, 그렇지 않을 경우 오른쪽으로 이동한다. 위 예시 그림의 경우엔 왼쪽으로 이동하게 된다.
그렇게 되면 i는 값이 그대로 이동하고, k 값은 왼쪽 sub-tree의 증강 값에 맞춰서 업데이트 된다.

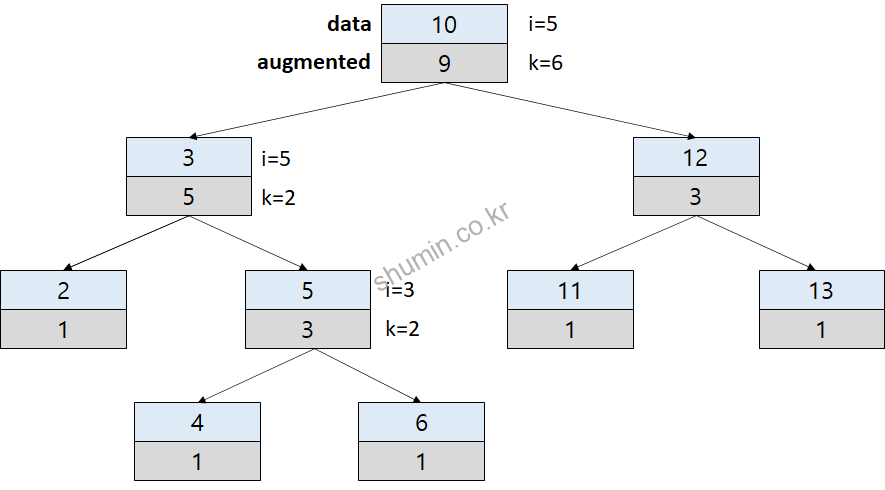
만약 i > k 일 경우에 오른쪽으로 이동하게 되면 i값도 변하게 된다. i의 값은 i-k 의 값이 저장된다.

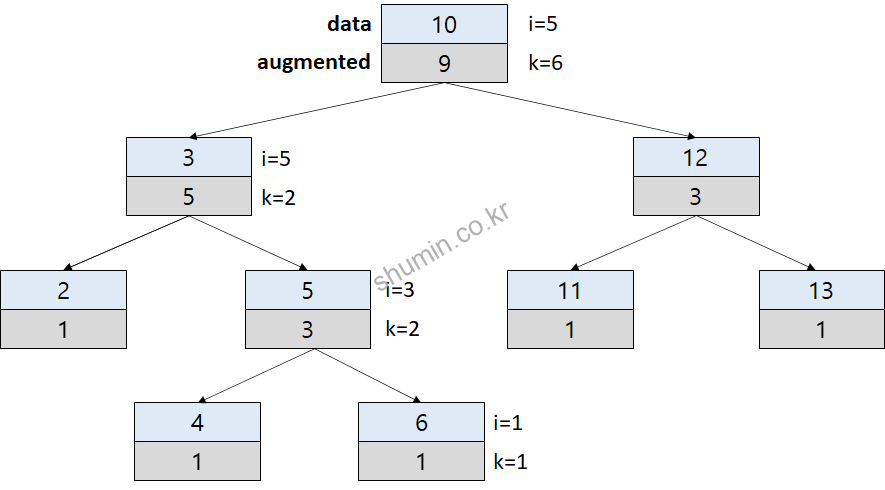
최종적으로 i와 k가 같은 값이 될 때가 우리가 찾고자 하는 노드가 된다. RB tree에 비해서 메모리를 조금 더 사용해서 추가적인 탐색 기능이 들어간 것이다.

추가로 고려해야 할 부분은, 노드 삽입이 될 때는 augmented 값 또한 업데이트를 해줘야한다. 새로운 노드가 들어 갈 때는 반드시 지나온 node에 대해서 augmented 값을 1을 더해줘야 한다. 그러나 RB tree일 경우 rotate_left 또는 rotate_right 동작을 수행하게 되면 구조가 변경되어 augmented 값이 맞지 않는 상황이 생긴다.

RB Tree 적용

RB tree에 대해서 augmented 값을 다시 구하기 위해서 rotate 동작이 일어날 때는 반드시 recompute가 수행되어야 한다. 만약 recopute 동작이 수행되지 않으면 다음과 같이 augmented 값이 잘못된 값으로 저장 될 수 있다.

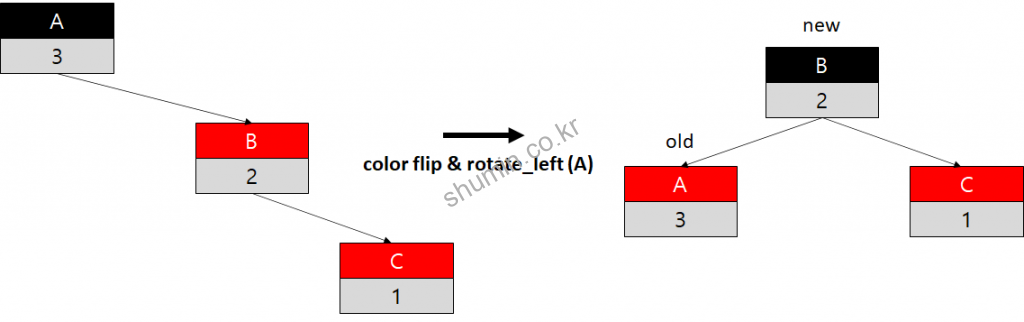
Kernel Code 분석

실제 최신 Kernel code에서 사용되는 augmented 값을 반영하는 코드 부분을 분석해본다. 우선 우리가 주요하게 보고자 하는 rotate 부분만 보면 아래와 같이 매크로로 구성된다.

#define RB_DECLARE_CALLBACKS(rbstatic, rbname, rbstruct, rbfield,   \
                 rbtype, rbaugmented, rbcompute)        \
static void                             \
rbname ## _rotate(struct rb_node *rb_old, struct rb_node *rb_new)   \
{                                   \
    rbstruct *old = rb_entry(rb_old, rbstruct, rbfield);        \
    rbstruct *new = rb_entry(rb_new, rbstruct, rbfield);        \
    new->rbaugmented = old->rbaugmented;                \
    old->rbaugmented = rbcompute(old);              \
}                                   \
...

위 코드를 보면 우선 rbstatic 부분에 static을 써주면 static 함수가 되는 것이고, 그렇지 않으면 dynamic 타입으로 함수가 생성된다.

두 번째 define문 인자인 rbname은 함수의 이름을 생성해주는데, 만약 shumin 이라고 입력하게 되면 rotate 함수는 shumin_rotate라는 이름의 함수가 생성된다. 참고로 ##는 좌우의 문자열을 이어준다.

세 번째 인자인 rbstruct는 우리가 사용하는 구조체 타입인 INFO를 넣어주면 된다.

네 번째 인자인 rbfield는 노드를 구성하는 포인터인 변수를 말한다. 우리는 node라고 지었다.

다섯 번째 인자인 rbtype은 augmented의 타입을 말하기 때문에, 우리는 int라고 적어주면 된다.

여섯 번째 인자인 rbaugmented는 우리가 사용하는 구조체 내부에 augmented 값을 가리키는 변수명을 말한다. 우리는 augmented라고 지었다.

마지막 일곱 번째 인자인 rbcompute는 우리가 구현해야 될 recompute 함수명을 말한다.

따라서 new에는 기존 old의 augmented 값이 저장되고, old에는 recompute 함수의 결과가 저장되어 최종적으로 아래와 같이 define을 작성하게 되면 함수가 새로 생성된다.

#define RB_DECLARE_CALLBACKS(static, my_augment, INFO, node,  \
                 int, augmented, my_recomute)

static void                             \
my_augment_rotate(struct rb_node *rb_old, struct rb_node *rb_new) \
{                                   \
    INFO *old = rb_entry(rb_old, INFO, node);       \
    INFO *new = rb_entry(rb_new, INFO, node);       \
    new->augmented = old->augmented;                \
    old->augmented = my_compute(old);             \
}              

실제 컴파일 log를 아래와 같이 보면 my_augment 구조체가 어떻게 구성되는지 볼 수 있다. 구조체 내부에 새로 생성된 함수가 존재하는데, 이를 등록하는 함수가 존재하지 않기 때문에 함수를 등록하는 부분을 추가를 해줘야 한다.

$ gcc rb_tree.c rbtree.c -E

static inline void my_augment_propagate(struct rb_node *rb, struct rb_node *stop) { while (rb != stop) { INFO *node = ({ const typeof( ((INFO *)0)->node ) *__mptr = (rb); (INFO *)( (char *)__mptr - ((size_t)&((INFO *)0)->node) );}); int augmented = my_compute(node); if (node->augmented == augmented) break; node->augmented = augmented; rb = ((struct rb_node *)((&node->node)->__rb_parent_color & ~3)); } } static inline void my_augment_copy(struct rb_node *rb_old, struct rb_node *rb_new) { INFO *old = ({ const typeof( ((INFO *)0)->node ) *__mptr = (rb_old); (INFO *)( (char *)__mptr - ((size_t)&((INFO *)0)->node) );}); INFO *new = ({ const typeof( ((INFO *)0)->node ) *__mptr = (rb_new); (INFO *)( (char *)__mptr - ((size_t)&((INFO *)0)->node) );}); new->augmented = old->augmented; } static void my_augment_rotate(struct rb_node *rb_old, struct rb_node *rb_new) { INFO *old = ({ const typeof( ((INFO *)0)->node ) *__mptr = (rb_old); (INFO *)( (char *)__mptr - ((size_t)&((INFO *)0)->node) );}); INFO *new = ({ const typeof( ((INFO *)0)->node ) *__mptr = (rb_new); (INFO *)( (char *)__mptr - ((size_t)&((INFO *)0)->node) );}); new->augmented = old->augmented; old->augmented = my_compute(old); } static const struct rb_augment_callbacks my_augment = { my_augment_propagate, my_augment_copy, my_augment_rotate };

우리가 원하는 augmented 값을 recompute 하는 함수가 적용될 수 있도록 기존에 사용되던 함수를 augmented 향 함수로 업데이트 해줘야한다.

//  rb_insert_color(&info->node, root);
    rb_insert_augmented(&info->node, root, my_augment);

구현

삽입

int my_compute (INFO *i) {
    int sum = 0;
    int child_augmented;
    if(i->node.rb_left) {
        child_augmented = rb_entry(i->node.rb_left, INFO, node)->augmented;
        sum += child_augmented;
    }   
    if(i->node.rb_right) {
        child_augmented = rb_entry(i->node.rb_right, INFO, node)->augmented;
        sum += child_augmented;
    }   
    return sum+1;
}

RB_DECLARE_CALLBACKS( static, my_augment, INFO, node, int, augmented, my_compute)

int rb_insert(struct rb_root *root, INFO *info) {
    struct rb_node **p = &root->rb_node;
    struct rb_node *parent = 0;
    INFO *temp;
    while(*p) {
        // Container_of
        parent = *p; 
        temp = rb_entry( parent, INFO, node);

        if(strcmp(temp->data, info->data) > 0)
            p = &(*p)->rb_left;
        else if(strcmp(temp->data, info->data) < 0)
            p = &(*p)->rb_right;
        else
            return 0;
        temp->augmented++;
    }   
    info->augmented = 1;
    // Insert node
    rb_link_node(&info->node, parent, p); 
    // Recompute augmented
    //my_augment_propagate(parent, 0);
    // Balance tree
//  rb_insert_color(&info->node, root);
    rb_insert_augmented(&info->node, root, &my_augment);

    return 1;
}

탐색

탐색을 위해서 새로 함수를 추가해서, 처음 증강 트리를 소개했던 방식대로 i와 k를 이용해서 탐색을 할 수 있다. 물론 위와 같이 탐색을 하기 위해선 항상 augmented 값은 정확히 계산이 되어야 한다.

INFO *my_select( struct rb_node *node, int i )
{
    int k=1;
    if(node == 0 )
        return 0;

    if( node->rb_left )
        k = rb_entry(node->rb_left,INFO,node)->augmented+1;

    if( i==k )
        return rb_entry( node, INFO, node );

    if( i<k )
        my_select( node->rb_left, i );
    else
        my_select( node->rb_right,i-k);
} 

int main() {
    struct rb_root root = {0};
    int a[] = {1, 2, 3, 4, 5, 6, 7, 8};
    int i, index;
    INFO info[INFO_NUM] = {{"A",}, {"B",}, {"C",}};
    INFO *info_temp;

    for(i=0; i<INFO_NUM; i++) {
//      info[i].data = a[i];
        rb_insert(&root, info+i);
        display(&root);
    }
    while(1) {
        printf("Index: ");
        scanf("%d", &index);
        info_temp = my_select(root.rb_node, index);
        if(info_temp)
            printf("%dth Data=%s\n", index, info_temp->data);
        else
            printf("Out of range\n");
    }
    return 0;
}

이번엔 몇 번째로 높은 순서가 아니라, 특정 데이터가 몇 번째로 높은지를 탐색 하는 함수를 소개한다.

1. 찾고자 하는 노드의 k값 얻기
2. 해당 노드의 부모의 left의 k값에 1을 더하고, 찾고자 하는 노드의 k값과 더하기
3. 찾고자 하는 노드의 포인터를 부모의 포인터로 업데이트

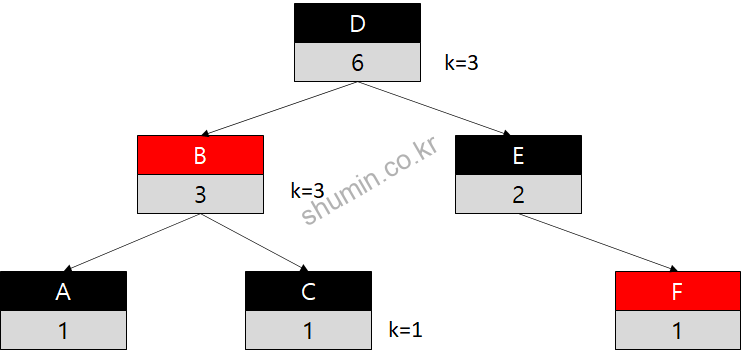
이를 Pseudo code로 변환하면 아래와 같다.

int my_rank (x) {
    k <- size[left[x]]+1;

    while(x != 0) {
        if (x->parent->right == x)
            k += size[x->parent->left]+1;
        x = x->parent;
    }
    return k;
}

실제로 C code로 구현을 하면 아래와 같다.

int my_rank(struct rb_node *node) {
    int k=1;

    if(node->rb_left)
        k = rb_entry(node->rb_left, INFO, node)->augmented+1;

    while(rb_parent(node) != 0) {
        if(rb_parent(node)->rb_right == node)
            if(rb_parent(node)->rb_left)
                k += rb_entry(rb_parent(node)->rb_left, INFO, node)->augmented + 1;
            else
                k++;
        node = rb_parent(node);
    }
    return k;
}