간격 트리 (Interval Tree)
Kernel에서도 많이 쓰이는 구조로, key 값으로 특정 하나의 값이 아니라 구간이 들어간다. Interval tree는 OS에서 프로세스 address영역을 관리 할 때 용이하게 쓰인다.
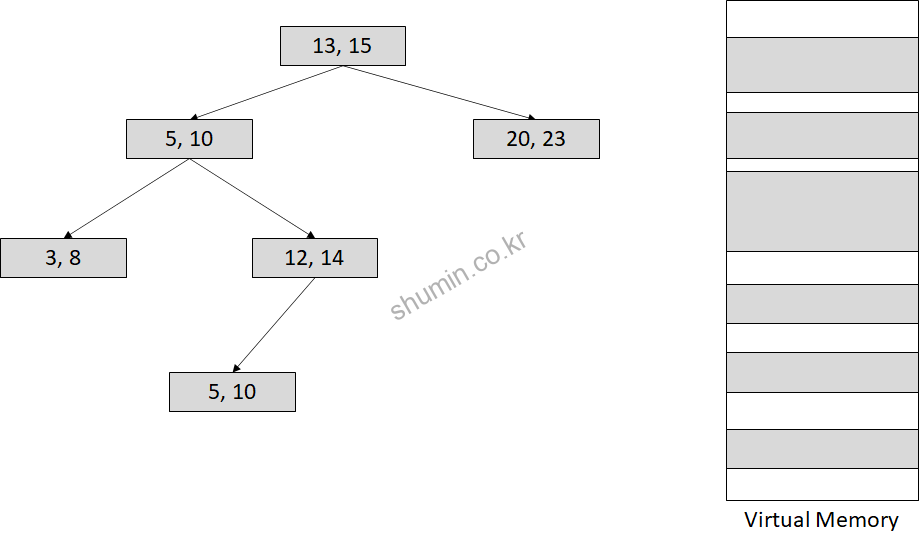
만약 위와 같은 tree 구조가 있을 때, 특정 구간 (예를 들면 [12 ~ 13])이 포함되어 있는지를 확인 할 것이다. 이 때도 augmented tree와 동일하게 augmented 값을 활용한다.
Interval tree의 경우엔 key 값이 2개이기 때문에, 그 중에 큰 값을 augmented 값으로 사용한다. 그리고 만약 sub-node가 2개 이상 존재할 때는 augmented 값 중 큰 값을 사용한다. 이 내용을 적용해서 다시 tree를 보면 아래와 같다.
구현
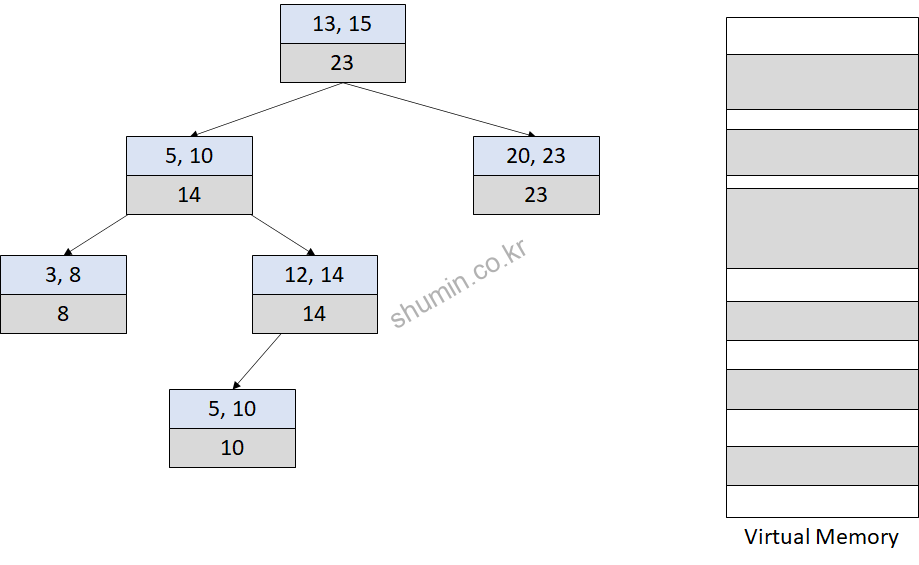
Interval tree의 각 노드가 어떻게 구성되어 있는지 보면 1) 시작 값, 2) 마지막 값, 3) augmented 값으로 구성된다.
struct interval_tree_node {
struct rb_node rb;
unsigned long start; /* Start of interval */
unsigned long last; /* Last location _in_ interval */
unsigned long __subtree_last;
};
Interval tree를 augmented RB tree에서 확장해서 사용하기 위해선 augmented 값을 기존 방식 (모든 sub-tree의 augmented의 합에 1을 더한 값)에서 업데이트를 해야한다. 이를 위해서 Kernel code에선 자동으로 함수를 생성하도록 define구문을 사용한다.
INTERVAL_TREE_DEFINE(struct interval_tree_node, rb, unsigned long, __subtree_last, START, LAST,, interval_tree)
#define INTERVAL_TREE_DEFINE(ITSTRUCT, ITRB, ITTYPE, ITSUBTREE, ITSTART, ITLAST, ITSTATIC, ITPREFIX)
/* Callbacks for augmented rbtree insert and remove */ \
\
static inline ITTYPE ITPREFIX ## _compute_subtree_last(ITSTRUCT *node) \
{ \
ITTYPE max = ITLAST(node), subtree_last; \
if (node->ITRB.rb_left) { \
subtree_last = rb_entry(node->ITRB.rb_left, \
ITSTRUCT, ITRB)->ITSUBTREE; \
if (max < subtree_last) \
max = subtree_last; \
} \
if (node->ITRB.rb_right) { \
subtree_last = rb_entry(node->ITRB.rb_right, \
ITSTRUCT, ITRB)->ITSUBTREE; \
if (max < subtree_last) \
max = subtree_last; \
} \
return max; \
}
위 예시 코드는 interval_tree.c와 interval_tree_generic.h에서 발취해왔다. 위 코드가 실제 pre-processor를 거치게 되면 아래와 같은 코드가 될 것이다.
unsigned long interval_tree_compute_subtree_last(struct interval_tree_node *node)
{
unsigned long max = (node)->last, subtree_last;
if (node->rb.rb_left) {
subtree_last = rb_entry(node->rb.rb_left,
struct interval_tree_node, rb)->__subtree_last;
if (max < subtree_last)
max = subtree_last;
}
if (node->rb.rb_right) {
subtree_last = rb_entry(node->rb.rb_right,
struct interval_tree_node, rb)->__subtree_last;
if (max < subtree_last)
max = subtree_last;
}
return max;
}
위 코드를 보면 왼쪽과 오른쪽 sub-tree에서 max 값을 찾아서 큰 값을 찾아내는 함수를 볼 수 있다. 여기서 중요한 점은 삽입 할 때는 start 값을 가지고 좌우 탐색을 진행하며, augmented 값을 업데이트 할 때는 last 값을 사용한다.
탐색
예제를 통해서 Interval tree에서 탐색되는 과정을 보면 아래 그림과 같다.
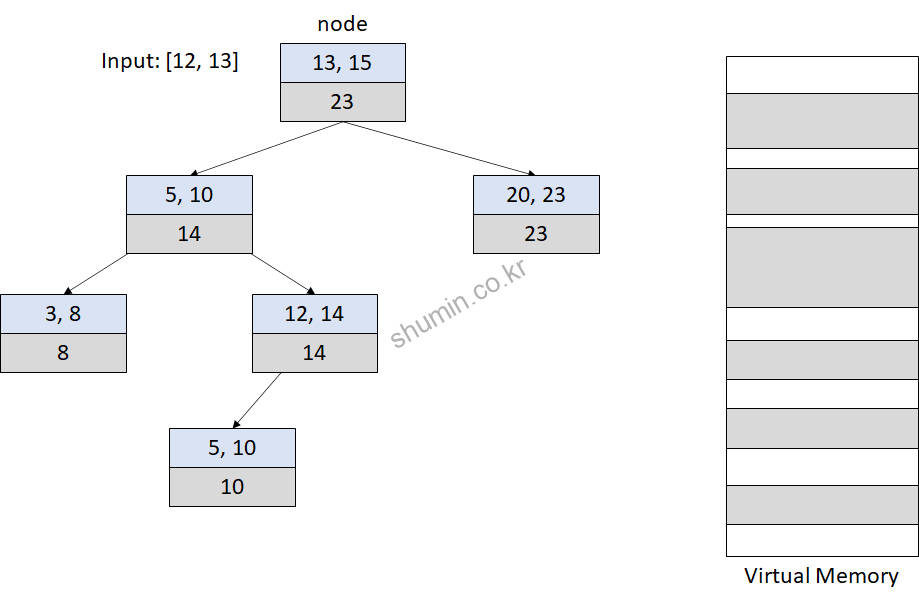
우선 root node에서 left node가 있는지를 보고, 있다면 start값 (12)과 node->rb.rb_left값 (14)를 비교한다. 만약 참이면 왼쪽 sub-tree로 이동한다. 만약 왼쪽 sub-tree의 augmented 값이 10이라고 하면 왼쪽에 대해서 검색하지 않을 것이다.
그리고 다시 왼쪽 sub-tree의 augmented 값과 비교하게 될텐데, 이때 12보다 작은 8이기 때문에 현재 node의 값을 비교해본다. node->start <= last (5 <= 13)가 참이 되고, start <= node->last (12 <= 10)가 참이 되지 않는다. 이때 오른쪽 노드를 검색해서 존재하면 오른쪽으로 node가 이동한다. start <= node->__sub_tree_last (12 <= 14)조건에 만족하기 때문에 continue구문을 수행한다.
다시 왼쪽 sub-tree가 존재하는지 보고 값을 확인해도 start <= left->__sub_tree_last 조건을 만족하지 않으면서, 다음 조건인 node->start <= last를 만족하면서 [12, 14]를 가리키는 노드를 return 한다.
struct interval_tree_node *
interval_tree_subtree_search(struct interval_tree_node *node, unsigned long start, unsigned long last) {
while (true) {
if (node->rb.rb_left) {
struct interval_tree_node *left = rb_entry(node->rb.rb_left,
struct interval_tree_node, rb);
if (start <= left->__sub_tree_last) {
node = left;
continue;
}
}
if (node->start <= last) {
if (start <= node->last)
return node;
if (node->rb.rb_right) {
node = rb_entry(node->rb.rb_right,
struct interval_tree_node, rb);
if (start <= node->__sub_tree_last)
continue;
}
}
return NULL;
}
}
Interval tree는 process 할당 영역, disk 영역 등등 지금은 선형 구간에서 많이 쓰이고 있지만, 면이나 입체에서도 쓰면 충돌 감지도 할 수 있다.
최종적으로 노드 삽입과 검색을 위한 테스트 코드는 아래와 같다.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "interval_tree.h"
#include "rbtree_augmented.h"
#include "interval_tree_generic.h"
#define INFO_NUM 6
struct interval_tree_node *
interval_tree_subtree_search(
struct interval_tree_node *,
unsigned long, unsigned long);
typedef struct {
unsigned long start;
unsigned long last;
unsigned long __subtree_last;
int color;
} NODE_INFO;
int __display(struct rb_node *temp, NODE_INFO (*array)[10], int *row, int *col) {
struct interval_tree_node *info;
if(temp == 0)
return 0;
++*row;
__display(temp->rb_left, array, row, col);
info = rb_entry(temp, struct interval_tree_node, rb);
array[*row][(*col)].color = rb_color(temp);
array[*row][(*col)].start = info->start;
array[*row][(*col)].last = info->last;
array[*row][(*col)++].__subtree_last = info->__subtree_last;
__display(temp->rb_right, array, row, col);
--*row;
}
void display(struct rb_root *root) {
int row = -1;
int col = 0;
NODE_INFO a[10][10] = {0,};
__display(root->rb_node, a, &row, &col);
system("clear");
for(int i=0; i<10; i++) {
for(int j=0; j<10; j++) {
if(a[i][j].__subtree_last) {
if(a[i][j].color == RB_RED)
printf("<%2lu,%2lu,%2lu>", a[i][j].start, a[i][j].last, a[i][j].__subtree_last);
else
printf("[%2lu,%2lu,%2lu]", a[i][j].start, a[i][j].last, a[i][j].__subtree_last);
}
else
printf("%10c", ' ');
}
printf("\n");
}
getchar();
}
int main() {
struct rb_root root = {0};
int i, index;
struct interval_tree_node *temp;
struct interval_tree_node nodes[INFO_NUM] = {
{{0,},13,15,},
{{0,},5,10,},
{{0,},20,23,},
{{0,},3,8,},
{{0,},12,14,},
{{0,},5,10,},
};
display(&root);
for(i=0; i<INFO_NUM; i++) {
interval_tree_insert(nodes+i, &root);
display(&root);
}
temp = interval_tree_subtree_search( nodes, 12, 13 );
if( temp )
printf("%lu,%lu\n", temp->start, temp->last);
else
printf("%lu,%lu\n", 12UL, 16UL);
return 0;
}